量子力学の基礎概念
10.1 運動量の観測モデルのシミュレーション
前節では、運動量の観測モデルの欠陥を波束を用いることにより修正することができた。本節では、波束を用いて確率密度を計算し、観測の様子をシミュレーションしてみる。まず、シミュレーションの前提について説明する。
まず、計算を簡単にするためにここからは原子単位系を用いる。(電子の質量=電子の電荷=光の速さ=ћ=1)これにより、基礎となる式は次のようになる。なお、観測の対象を電子である。
ψA+ (y , t)=C∫dkφ(k)exp{(i⊿t)(αykn - αξk)+iky-itћ(k+αkn⊿t)2/2} (10.1)
ψA- (y , t)=C∫dkφ(k)exp{(i⊿t)(-αykn - αξk)+iky-itћ(k-αkn⊿t)2/2} (10.2)
次に、前節では特に指定しなかった波束φ(k)をガウス波束とする。なお、シミュレーションで数値的に規格化を行うため、規格化定数を考慮する必要はない。
φ(k)=exp(-k2/2σ2) (10.3)
さて、式(10.3)を式(10.1)及び式(10.2)代入し、本HPの「ボーム力学 1.4 ガウス波束」で用いた次の公式によりそれぞれ積分が実行できる。
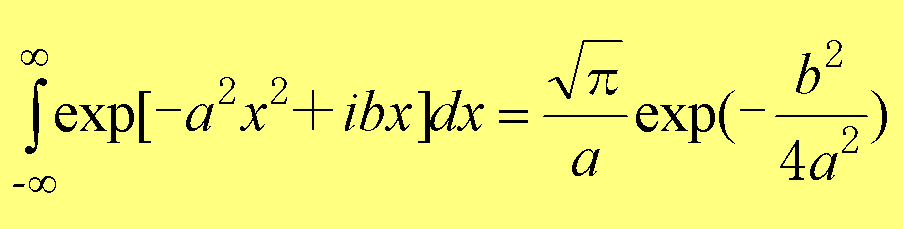
そして、求めたψA+ (y , t)とψA- (y , t)を重ね合わせ、複素共役との積を求め確率分布を計算した。この計算過程は、非常に煩瑣でありあまり意味の無いものであるのでここでは省略する。なお、衝撃的相互作用を用いていることから、⊿t2=0とした。また、この計算過程は本HPの「ボーム力学 1.5 二重スリット1」で二重スリットの干渉像の確率密度を計算する過程と類似し、シミュレーション結果で明らかになるように、運動量がうまく観測できないケースでは、観測対象であるx軸上の運動量重ね合わせの状態が観測過程に反映され、y軸上で+方向と-方向に進行する波束の干渉が表れる。
さて、前節の最後で説明したように、波束の平均的な運動量⊿p0が観測対象の運動量より十分に大きくないと、正確な観測ができない。つまり、
αkn⊿t>>⊿p0 (10.4)
が正確な観測の条件である。そして、本シミュレーションでは式(10.3)の波束を用いていることから、⊿k0=σであり、原子単位系を用いていることから⊿p0=⊿k0=σとなる。従って、
αkn⊿t>>σ (10.5)
が観測の条件となる。
10.2 シミュレーションの結果
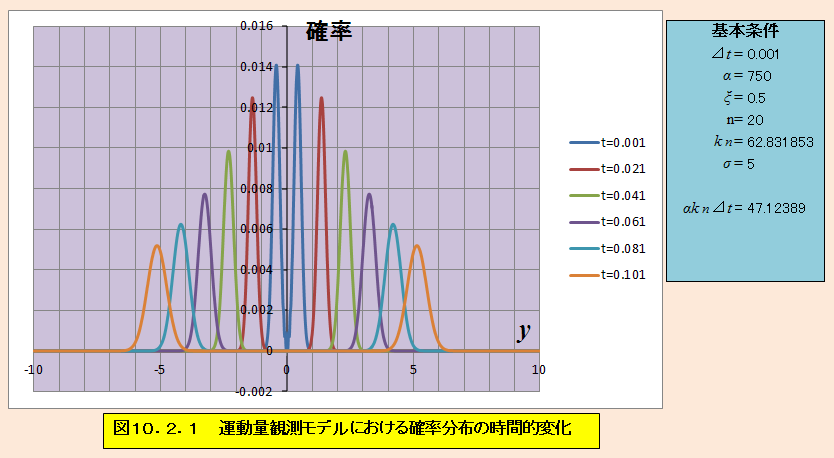
まず、図10.2.1が観測がうまく行くケースの例である。衝撃的相互作用が終ると同時に正方向(右方向)と負方向(左方向)に波束が表れ、そのまま若干広がりながら離れていることがわかる。なお、全てのシミュレーションで、衝撃的相互作用の時間は⊿t=0.001とした。また、前節の最初に近似したようにkn>>Lであることから、全てのシミュレーションでn=20、L=1.0とした。
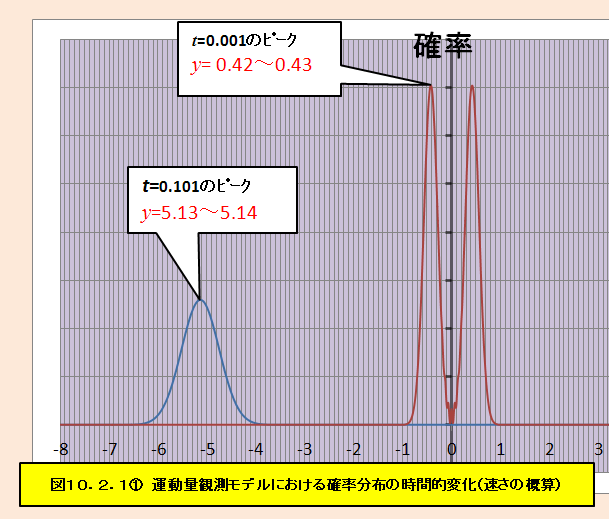
これは、前節の計算で示された様子を表しているが、波束の速さが前節の式(9.10)のとおり、
vy+= αkn⊿t/mであるかを試算してみると、図10.2.1のように波束の速さは、vy+=47.0~47.2であり αkn⊿t=47.12389と同程度であることがわかる(原子単位系なのでm=1)。徐々に、αkn⊿tを小さくして結果を示すと図10.2.2~図10.2.9のようになり、式(10.5)の観測条件を満たさなくなるにつれて、左右の波束が干渉していくことがわかる。確率密度が単純に重ね合わせにならないのは波動関数が干渉項を有するためであり、量子的な性質の表れである。これは、本質的に二重スリットにおける干渉像と同じものであるが、どのような現象なのか対比してみる。
まず、観測対象はx軸上の運動量重ね合わせの状態(knと-kn)であり、二重スリットならばいずれの開口部も空いた状態に対応する。しかし、いずれの開口部も空いた状態なら干渉が生じるはずであるが、図10.2.1や図10.2.2では生じていない。これは、二重スリットに対比すれば、どちらを粒子が通ったかを観測したことに対応する。
そうすると、図10.2.1や図10.2.2では、左右に進行する波束が存在しているが、衝撃的相互作用が終わった後(t >⊿t)に感光板などで観測を行うと、どちらの波束が実際に観測されるかが定まっているのだろうか?もし、定まっているなら観測されない方の波束は何なんだろうか?
この疑問については正に量子力学の解釈の問題であり、断定的にこうであるということはできない。しかし、恐らく標準的と思われる観測による波束の収縮(射影公準)を仮定する解釈に拠るなら、観測の瞬間に左右どちらかの波束に状態が確定し、観測されない方の波束はその瞬間に消滅すると考えられる。なお、エレベット解釈に拠れば左に観測する世界と右に観測する世界に世界が分岐すると解釈さるためどうとも言えず、またアンサンブル解釈(「波動関数は同じやり方で準備された系のアンサンブルの集団に関する記述である」という解釈)に拠れば、左右どちらの運動量かは最初から決まっており、波動関数は個別系を記述するものではないのだから観測されない方の波束は問題にならない。さらに、軌跡解釈(ボーム力学)に拠れば、初期状態で粒子(この解釈は粒子の存在を認める)が有する運動量は0で、観測の過程で粒子が運動量を有することとなり、また観測されない方の波束は空の波束としてその後も存在することとなる。(詳細は、このホームページのボーム力学を参照。)
次に、図10.2.6と図10.2.7を見ると、ピークがそれ程強くは無いが激しく干渉を起こした後に、波束が左右に進行していることがわかる。感光板などを用いると左右のどちらかで粒子(粒子のような痕跡)が観測されるが、二重スリットに対比すれば干渉を起こした1点がスクリーンに出現したことに対応し、結局どちらのスリットを通ったかはわからない。従って、図10.2.7の波束でy軸上の運動量は観測されても、x軸上の運動量が観測されたことにはならない。ただし、軌跡解釈では初期状態で粒子が有する運動量は0であるものの、x軸上のどこに粒子があったかに応じy軸上のどちらに粒子が表れるかを計算することができるという点で事情が異なる。この点は、軌跡解釈を二重スリットに適用した場合、スリットの右を通ればスリットの中心を境にスクリーンの右側に粒子が表れ、スリットの左を通れば左側に粒子が表れるということを計算できることに類似している。
前節及び本節では、「運動量の観測モデル」というかなり具体的な例を取り上げたが、次節ではもう少し抽象的なモデルを取り上げることとする。(HI=gApyという衝撃的相互作用を用いて、物理量Aと検針器の振れyを相関させるモデル)
αkn⊿t=47.12389 σ=5
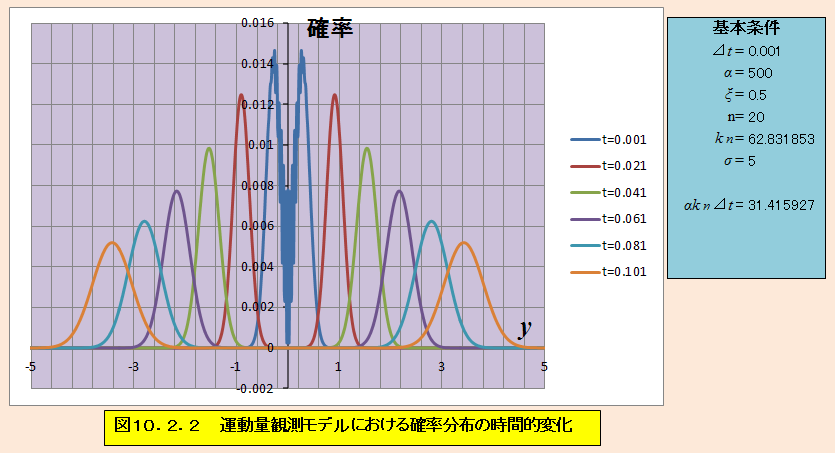
αkn⊿t=31.415927 σ=5
これぐらいの干渉なら、ほとんど正確な測定ができるだろう。
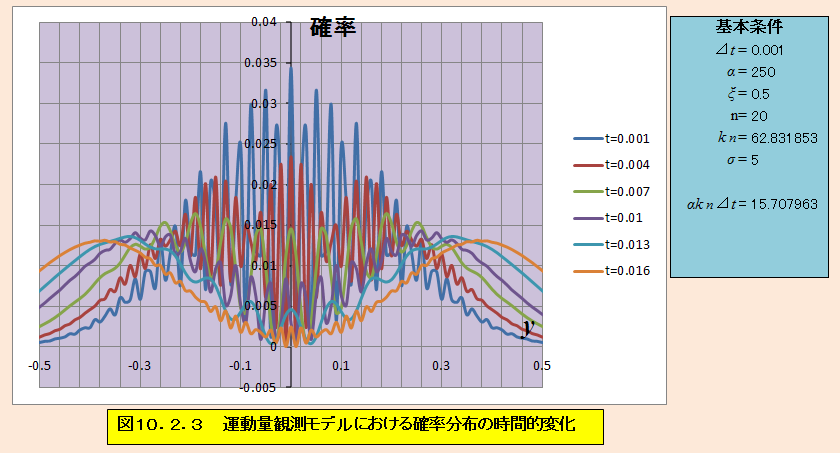
αkn⊿t=15.707963 σ=5
干渉が強く表れており、これでは正確な観測はできないだろうと思ったら、左右に波束が表れた。
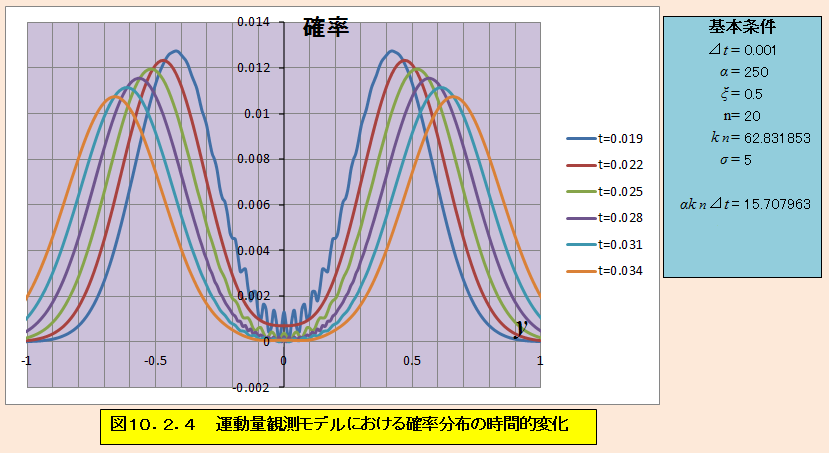
αkn⊿t=9.424778 σ=5
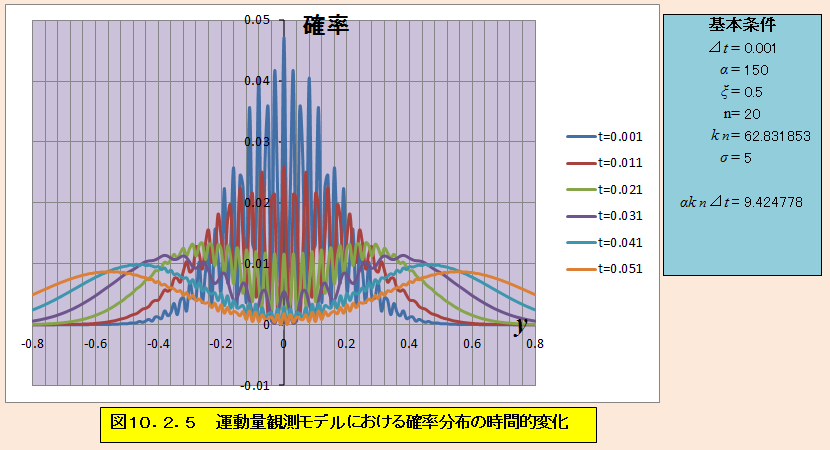
αkn⊿t=7.8539816 σ=5
一応波束ができたけど・・・・
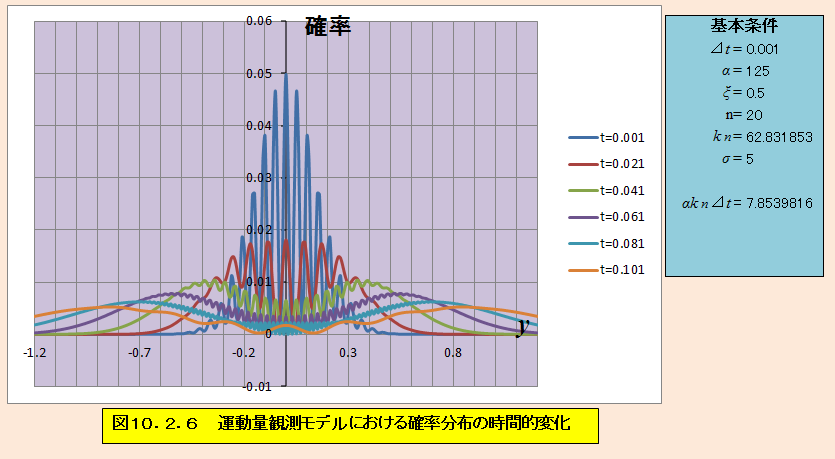
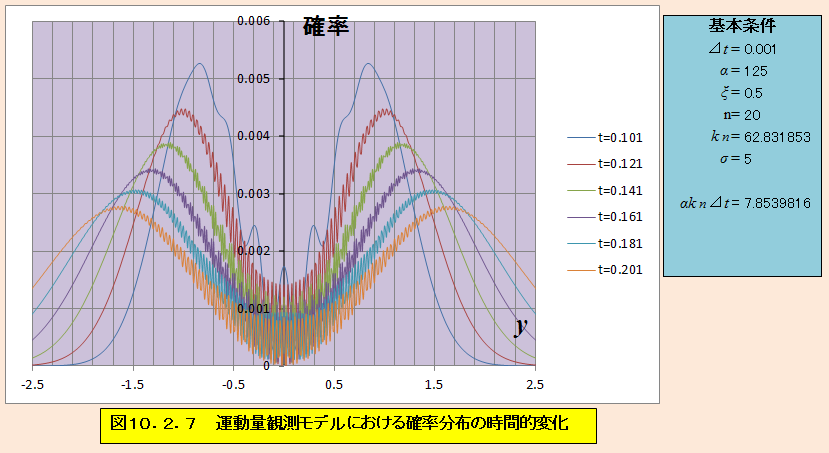
αkn⊿t=4.712389 σ=5
波束の広がりと進行の区別が付かない。
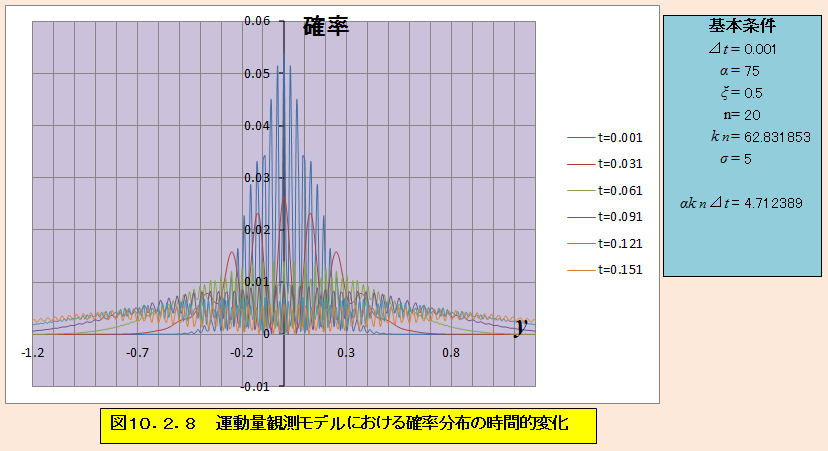
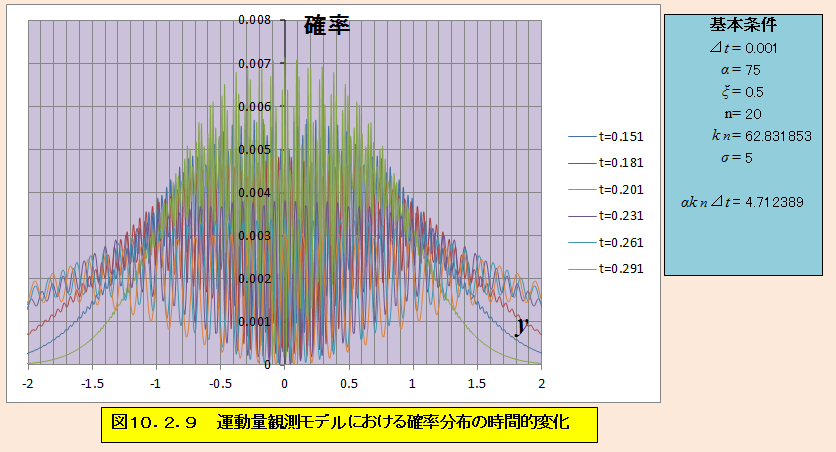
アマチュアリズムの量子力学