�ʎq�͊w�̊�b�T�O
�W�D�P�@�^���ʂ̊ϑ����f���@
�@�����ł́A�ϑ��ߒ��̗��_����̓I�ȃ��f���ɓK�p���Ă݂�B�悭�m���Ă������̓V���e�����E�Q�����b�n�̎����ł��邪�A����ɂ��Ă͌�q���邱�ƂƂ��A�����ł͎����I���W�i���ɍl�Ă����A���^�|�e���V�����̔g������p�����ȒP�ȃ��f���ɓK�p���Ă݂邱�ƂƂ���B�Ȃ��A��q����悤�ɂ��̃��f���ɂ͌��ׂ����邪�A�ϑ��ߒ��̗��_����̓I�ȃ��f���ɓK�p�����l�q�𗝉����邱�Ƃ͂ł���B
�@�܂��A0��x��L�ɂ�����P�������^�|�e���V�����̔g������S(x)�́A�K�i�����q�������āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��S(x)��sin(n��x/L)��sin(knx)��(exp(iknx)�|exp(-iknx))�^2i �@
(8.1)
(kn��n��/L �Ƃ����B�j
�ł���B��(8.1)�̍ʼnE�ӂ����Ă݂�ƁA�K�i�����q�������āAexp(iknx)�Ɓ|exp(-iknx)�Ƃ����Q�̉^���ʌŗL���̏d�ˍ��킹�̏�Ԃł���A�ŗL�l�����ꂼ��ћkn��-ћkn�ł��邱�Ƃ��킩��B�܂�A�P�������^�|�e���V�����̔g������S(x)�́A�^����ћkn��-ћkn�̏d�ˍ��킹�̏�Ԃł���ƌ��邱�Ƃ��ł���B
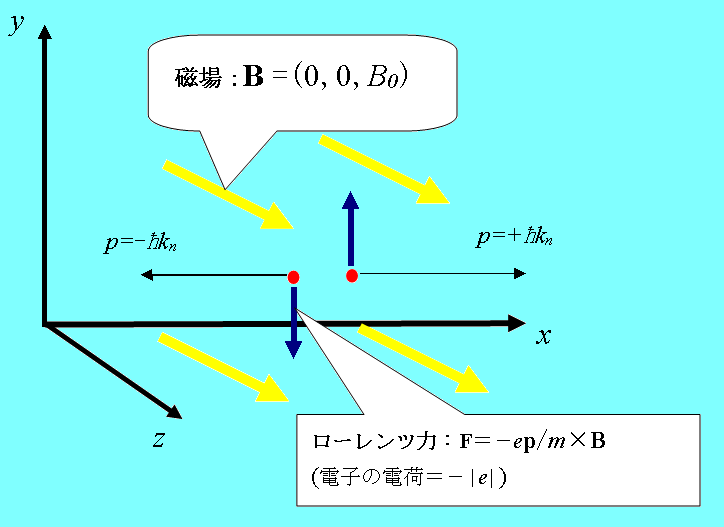
�@���āA�����Ōn�̑Ώۂ�d�q�ł��邷��Ax�����Ɛ�����z��������Z�����Ԃ��������������ƁA���[�����c�͂ɂ��y�����ɉ^���ʂ�L�����Ԃ������邱�Ƃ��\�z�����B����ɁA�^���ʂ�y�����͉^���ʂ�x�����������ɂ���Đ����̂����ꂩ�̕����ƂȂ邩�����܂邩��Axz���ʂƕ��s����y����̐��ƕ��̈ʒu���Q���̊�����ݒu����A�ÓT�I�ȑΏۂł��銴���Ƃ̑��ݍ�p�ɂ��g���̎��k�������āA�ǂ���̊������������邩�ɂ��A��S(x)�̉^���ʂ̕������ϑ��ł���悤�Ɏv����B

�@������V�����f�B���K�[�������ŕ\�������̂����A�܂��͌ÓT�I�ȃ��O���W�A�����狁�߂Ă݂�B���ꂪ����ۂ̃��O���W�A��L�́AA���x�N�g���|�e���V�����A-e��d�q�d�ׁA��m�d�q���ʂƂ���A
�@�@�@�@�@�@�@L �� mṙ 2 �^2 �|eṙ �A �@�@�@�@�@�@�@�@�@�@�@�@ (8.2)
�ł���B�������狤���^����p ����L�^��ṙ �����߂�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@p�@�� mṙ �|eA �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (8.3)
�ƂȂ邩��A�n�~���g�j�A��H�́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ H�@��
p�ṙ�|L�@��
p�(p + eA )/m�|(p
+ eA
)2
�^2m +
e(p + eA )
�A�^m
��
(2p2 +
2ep�A�|
p2�|2ep�A�|e2A2
+ 2ep�A +
2e2A2
)�^2m
��
(p2
+2ep�A +
2e2A2)�^2m
��
(p +
eA)2�^2m
(8.4)
�̂悤�ɂȂ�B�ʎq�͊w�I�ȃn�~���g�j�A�������߂�ɂ́Ap�ˁ|ћ���Ƃ����ϊ�������悭�A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ H�@��
(�|iћ��+
eA)2�^2m��(�|ћ2��2�|i
eћ���A�|i
eћA����|i
eћA���+
e2A2)�^2m
��(�|ћ2��2�|i
eћ���A�|2i
eћA���+
e2A2)�^2m
�ƂȂ�B����ɁA�N�[�����Q�[�W���Ƃ����A��0�Ƃ���A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@H ��(�|ћ2��2�|2i eћA���+ e2A2)�^2m �@�@�@�@ �@(8.5)
�ł���B�����ŁA�N�[�����Q�[�W���A��0���l�����āA�x�N�g���|�e���V��������̓I�ɒ�߂�ƁA�����z�����ɂ݂̂ň�l�ȑ傫��B�ł���Ƃ���AB�����~A�ł��邱�Ƃ��A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@A��(-By/2 , Bx/2 , 0) (8.6)
�ƂȂ�B�]���āA�n�~���g�j�A���́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@H�@��{�|ћ2��2 + i eћB(y��/��x�|x��/��y)+ e2B2(x2+y2)�^4}�^2m (8.7)
�ƂȂ�B
��(8.7)�̑�ꍀ�͖��炩�Ɏ��R���q�̃n�~���g�j�A���ł��邩��A�O�߂̎�(7.4)���瑊�ݍ�p�̊Ԃ͖������邱�Ƃ��ł��A����ɑ��ݍ�p�̒��O��y2≈0�Ƃ���A���ݍ�p�n�~���g�j�A��HI�́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ HI ��{ i eћB(y��/��x�|x��/��y)+ e2B2x2�^4}�^2m�@�@ (8.8)
�ƂȂ�B
���āA�����őO�߂̓��e�ƑΔ䂳����ƁA�ϑ��̑ΏۂƂȂ�I�u�U�[�o�u����Px�ŁA��(7.6)�̌ŗL�lm��ћkn�܂���-ћkn �A�ŗL��vm(x)��exp(iknx)�܂��́|exp(-iknx)�ł���A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@Pxexp(iknx)��ћknexp(iknx)
(8.9)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
Pxexp(-iknx)��-ћknexp(-iknx)
(8.10)
�ƂȂ�B�܂��A��(7.7)��HI(M,y)��x���ϐ��Ƃ��ĉ���邪�AHI(Px,y)�Ƃ��ĕ\���ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@HI(Px ,y ,x)��{ �| eByPx�| i eћBx��/��y+ e2B2x2�^4}�^2m�@�@�@ �@(8.11)
�ƂȂ�B����ɁA��(7.8)��Cm��1�Ƃ��邱�Ƃ��ł�(�^���ʂ����̌ŗL�����|exp(-iknx)�Ƃ�������)�A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ��S(x)��exp(iknx)�|exp(-iknx)�@�@�@�@�@�@�@ �@(8.12)
�ł���B(�K�i�����q���Ȃ���)
�@�����ŁA�ʎq�nA�̔g��������A����A(y ,t)�Ƃ���A��(7.9)�Ɠ��l�Ɍ����n�̔g������(x, y, t)��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ��(x ,y ,t)����A��S����A(y,t){exp(iknx)�|exp(-iknx)} (8.13)
�ƂȂ�A�V�����f�B���K�[�������́A
�@�@ iћ{exp(iknx)�|exp(-iknx)}(����A(y
, t)/��t)��HI(Px ,
y ,
x){exp(iknx)�|exp(-iknx)}��A(y
, t)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��{
�|
eByPx�| i eћBx��/��y+
e2B2x2�^4}{exp(iknx)�|exp(-iknx)}��A(y
, t)�^2m
�@���|
eByћkn{exp(iknx)�{exp(-iknx)}��A(y
, t)�^2m�{{exp(iknx)�|exp(-iknx)}{
�| i
eћBx�݃�A(y , t)/��y+
e2B2x2��A(y
, t)�^4}�^2m
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
(8.14)
�ƂȂ�B
�W�D�Q�@�V�����f�B���K�[�������̉��
�@�����ŁA��(8.14)�̉������߂������A�L�q���ȒP�ɂ��邽�߁A
�@�@�@�@�@�@�@�@����eBћ�^2m�@�@�@�@�@�@�@�@�@����e2B2�^8m (8.15)
�ƒu���ƁA��(8.14)�́A
iћ{exp(iknx)�|exp(-iknx)}(����A/��t)���|��ykn{exp(iknx)�{exp(-iknx)}��A�{{exp(iknx)�|exp(-iknx)}{�|i��x�݃�A/��y+
��x2��A}
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@�@�@�@ (8.16)�@
�ƂȂ�B�����ŁAexp(-iknx)�^L�̐ς��Ƃ�0��x��L�͈̔͂Őϕ�����ƁA
�@�@�@�@�@�@�@�@��exp(-iknx)exp(iknx)�^L dx��1 ��exp(-iknx)exp(-iknx)�^L dx��0
�@��xexp(-iknx)exp(iknx)�^L dx��L�^2 ��xexp(-iknx)exp(-iknx)�^L dx��iL�^2kn
��x2exp(-iknx)exp(iknx)�^L dx��L2�^3 ��x2exp(-iknx)exp(-iknx)�^L dx��iL�^2kn�{1�^2kn2
��p���邱�Ƃɂ��A
�@�@�@�@�@�@�@�@iћ����A+/��t���|��ykn��A+�|i���́݃�A+/��y+���ʃ�A+�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (8.17)
�@�@�@�@�@�@�@�@�@�@�i����L�^2�|iL�^2kn�@����L2�^3�|iL�^2kn�|1�^2kn2�@�j
�ƂȂ�B(���̏ꍇ����A����A+�Ƃ����B)
���l�ɂ��āA�|exp(iknx)�^L�̐ς��Ƃ�0��x��L�͈̔͂Őϕ������
�@�@�@�@�@�@�@ iћ����A-/��t����ykn��A-�{i����*�݃�A-/��y�{����*��A-�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (8.18)
�ƂȂ�B(���̏ꍇ����A����A-�Ƃ����B)�@�@
�����ŁA��(8.17)�̕��f�������Ƃ�ƁA
�@�@�@�@�@�@�@�@�@�@�@iћ����*A+/��t����ykn��*A+�{i����*�݃�*A+/��y+����*��*A+�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (8.19)
�ƂȂ�A��*A+����A-�@��*A-����A+�ł��邱�Ƃ��킩��B
��(8.17)�Ǝ�(8.18)�́A�`���I�ɉ���\�����Ƃ��ł��At��0�ő��ݍ�p������( 0, 0, B )�����������Ƃ����t����t�ł́A
�@�@�@�@�@�@�@�@��A+(y ,
��t)��exp(-i��t����/ћ)exp{(-i��t/ћ)(�|��ykn�|i���́�/��y)}��A(y
, 0)�@�@�@�@ �@(8.20)
�@�@�@�@�@�@�@�@�@�@�@�@ ��A-(y
,
��t)��exp(-i��t����*/ћ)exp{(-i��t/ћ)(��ykn�{i����*��/��y)}��A(y , 0)�@�@�@�@�@�@
(8.21)
�ƂȂ�B
�@�����ŁA��t≈0�Ȃ̂Ŏ�(8.19)����t�P���̃I�[�_�[�ŋߎ�����ƁA
�@�@�@�@�@�@�@�@�@�@�@�@��A+(y , ��t)≈exp(-i��t����/ћ){1�{i��t/ћ(��ykn�{i���́�/��y)}��A(y , 0) (8.22)
�ł���B������Ԃ�y�����̉^���ʂ�0�Ƃ���A����A(y , 0)/��y��0�ł��邩��A
�@�@�@�@�@�@�@�@��A+(y , ��t)≈exp(-i��t����/ћ)(1�{i��t��ykn/ћ)��A(y , 0) (8.23)
�ƂȂ�A(1�{i��t��ykn/ћ)≈exp(i��t��ykn/ћ)�Ƃ��ĉ^���ʌŗL�l�����߂�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@-iћ{����A+(y , ��t)/��y}/��A+(y , ��t)����t��kn����teBћkn�^2m�@�@�@�@�@�@�@�@�@�@�@ (8.24)
�ł���B���l�ɂ��āA��A-(y , ��t)�ɂ��ċ��߂�ƁA
�@�@�@�@�@�@�@�@-iћ{����A-(y , ��t)/��y}/��A-(y , ��t)���|��t��kn���|��teBћkn�^2m�@�@�@�@�@�@�@�@ (8.25)
�ƂȂ�A���ꂼ��̉^���ʂ̕������ÓT�I�ȃ��[�����c�͂ƈ�v���邱�Ƃ��킩��B
�@����A�g�����́A(1�{i��t��ykn/ћ)≈exp(i��t��ykn/ћ) �A(1�|i��t��ykn/ћ)≈exp(-i��t��ykn/ћ) �Ƃ����ߎ���p����ƁA
�@�@�@�@�@�@�@�@�@�@�@�@
��A+(y , ��t)≈exp(-i��t����/ћ)exp(i��t��ykn/ћ)��A(y
,
0)
(8.26)
�@�@�@�@�@�@�@�@�@�@�@�@�@��A-(y ,
��t)≈exp(-i��t����/ћ)exp(-i��t��ykn/ћ)��A(y
,
0)
(8.27)
�ł��邪�A������Ԃ�y�����̉^���ʂ�0�Ƃ���A����A(y ,
0)/��y��0�ł��邩��A���ꂪ�����ꍇ�̃n�~���g�j�A��
H'0 ���|ћ2��2/��y2�^2m����p������ƁA
�@�@�@�@�@�@�@�@�@
H'0 ��A+(y , ��t)��
(��t��kn)2ћ�^2m
��A+(y ,
��t) (8.28)
H'0 ��A-(y , ��t)��
(��t��kn)2ћ�^2m
��A-(y ,
��t)
(8.29)
�ƂȂ�A�������
H'0 �̌ŗL���ł���B�]���āAt����t�Ŏ��ꂪ�������Ă����̌���A+(y ,
��t)�@��A-(y ,
��t)�́A���Ԃɂ�鍀
(exp(-i(t�|��t)(��t��kn)2�^2m))���������ꂼ�ꎮ(8.26)��(8.27)�̔g�������ێ������B(�܂�A����Ԃł���)
����A�����n�̔g������t����t�ɂ����āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��(x ,y ,��t)��exp(iknx)��A+(y , ��t)�|exp(-iknx)��A-(y , ��t)�@�@�@�@�@�@�@�@�@ (8.30)
�ł���A�O�߂̎�(7.13)�⎮(7.14)�ɑ������邪�A�����H0���|ћ2��2 �^2m����p������ƁA
�@�@�@�@�@�@�@�@�@ H0��(x ,y ,��t)�� {ћ2kn�{(��t��kn)2ћ} �^2m ��(x ,y ,��t) (8.31)
�ƂȂ�AH0�̌ŗL���ł���B�]���āAt����t�Ŏ��ꂪ���������(x ,y ,��t)�́A���Ԃɂ�鍀(exp(-i(t�|��t){ћkn�{(��t��kn)2�^2m))�������A��(8.30)�̔g�������ێ������B�i�܂�A����Ԃł���)
���āA��(8.30)�̔g������(x ,y ,��t)�́A��S(x)�̏d�ˍ��킹�̏�Ԃ�ێ������܂ܒ���ԂƂ��Ď��Ԕ��W���邽�߁A���̂܂܂ł͉^���ʂ̕������ϑ����邱�Ƃ͂ł����A�ϑ����邽�߂ɂ͔g���̎��k���N�����K�v������B�O�߂̋c�_�ɂ��A�g���̎��k���N�����ɂ͌ÓT�I�Ȍn�Ƃ̑��ݍ�p���K�v�ł��������A�����ŌÓT�I�Ȍn�Ƃ��ėp������̂��Axz���ʂƕ��s����y����̐��ƕ��̈ʒu���u�����Q���̊����ł���B�܂�A�ǂ���̊����ɔ����_���\��邩(�d�q�����q���̍��Ղ��c����)�ɂ������A+(y , ��t)����A-(y , ��t)�̂����ꂩ����܂�A��(8.30)�̑��d�I�ȍ\���ɂ���
�@�@�@�@�@�@�@�@�@�@��(x ,y ,��t)�@�ˁ@�@exp(iknx)��A+(y , ��t)
�@�@�@�@�@�@�@�@�@�@�@�@�@��(x ,y ,��t)�@�ˁ@�|exp(-iknx)��A-(y , ��t)�@
�̂ǂ��炩�̎��k�������A��S(x)�ɂ�����^���ʂ̕������ϑ��ł���̂ł���B
�W�D�R�@���f���̌���
�@�ꉞ�A��̓I�ȃ��f���ɑO�߂̊ϑ��ߒ��̗��_��K�p�ł��Ă���悤�Ɍ����邪�A���̉^���ʂ̕������ϑ����郂�f���ɂ́A���ׂ�����B��A(y , 0) �ɑ��āA�ŏ���y2≈0�Ɖ��肵���ɂ��ւ�炸�Ay�����̉^���ʂ�0�Ƃ݂Ȃ��Ă��邪�A����͉^���ʂƈʒu�̗������m�肷�邱�ƂɂȂ�A�s�m�萫�������炱�̂悤�ȏ�Ԃ͑��݂��Ȃ��By2≈0�Ƃ���A�K�R�I�ɏ�����Ԃ���A(y , 0)�͉^���ʂ�L���邱�ƂɂȂ�A���������ћk0(k0�͐������������蓾��)�Ƃ���A��(8.24)�̉^���ʂ͑�܂��ɂ����āAћk0+��teBћkn�^2m�ƂȂ�Bk0�͐������������蓾��̂ł��邩��Ak0��0�� |k0| ����teBћkn�^2m�ł���ꍇ�ɂ�y�����̉^���ʂ͕��ƂȂ�Ay���̕��̈ʒu�ɂ��銴���ɔ��s�_�������邱�ƂɂȂ�A��S(x)�̉^���ʂ̕����͐������ϑ�����Ȃ��B����Ɠ������Ƃ́B��(8.25)�ɂ�������B
�W�D�S�@�^���ʂ̑傫��
��(8.24)��(8.25)�ɂ��^���ʂ̑傫����������Ă��邪�A���ꂪ�ÓT�I�ȗ��_�l�ƈ�v���邩���m�F���Ă݂�B
�@�܂��A��(8.3)�����Ԃɂ���������ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@dp/dt ��mdṙ/dt �|edA/dt ��mdṙ/dt �|e{��A/��t�{(��A/��x)vx�{(��A/��y)vy�{(��A/��z)vz} �@�@
�ƂȂ顂���Ɏ�(8.6)��A��������ƁA
dp/dt ��mdṙ/dt �|e{(B/2)vxey�| (B/2)vyex}
�ƂȂ邪�A������y�����݂̂����o���ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@dpy/dt ��md2y/dt2 �|e(B/2)vx
�ƂȂ�B���[�����c�͂������Ă���̂�����^���������́Amd2y/dt2 ��evxB�ƂȂ邽�߁A�����������ƁA
�@�@�@�@�@�@�@�@�@�@dpy/dt ��evxB �|e(B/2)vx��eBvx�^2���}eBћkn�^2m
�ƂȂ�B(�Ō�̍��́Avx���}ћkn�^m)����ɂ��A�����Ȏ���t����t�ł́A
�@�@�@�@�@�@�@�@�@�@py���}eBћkn��t�^2m
�ƂȂ�A��(8.24)��(8.25)�ƈ�v���邱�Ƃ��킩��B(�Ȃ��Apy�͋����^���ʂł��邩��py��mvy�ł��邱�Ƃɒ���)
�����ؽ�т̗ʎq�͊w