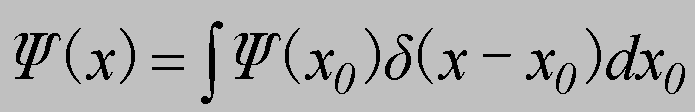量子力学の基礎概念

６．１　はじめに　

　先日(平成24年１月15日)のNature Physics電子版にて、「小澤不等式が正しい可能性が高いことが実験的に検証された。」旨が発表されたことを受け、私なりに行った小澤不等式の導出方法と意味の考察を説明する。(なお、6.3については何度か誤った導出方法を掲載したが、数名の閲覧者の方からご指摘を頂き最終的な形になりました。貴重なご指摘ありがとうございました。)

６．２　古典力学における位置と運動量の観測

　まず、古典力学における位置と運動量の観測について考察する。

　観測は観測装置によって行われるが、古典物理学の一般的なケースでは、観測装置が観測対象に及ぼす影響(観測装置と観測対象の相互作用)を無視するのが普通である。(例えば、鉄球の位置を観測する際に、太陽の光による影響は考えない。)

　しかし、ここでは次のような不完全な観測装置(Ｍ)があるとする。

�@　観測装置(Ｍ)は、位置と時間を同時に測定する。

「古典論では、観測対象は任意の時刻で確定した位置と運動量を有しているが、観測装置(Ｍ)から得られる測定値は、相互作用が生じているΔtの時間間隔のどの時点の位置と運動量を示すかはわからない。」

ということが言える。

　ではここで、ある粒子(S)の時刻t₀における位置と運動量を観測装置(Ｍ)を用いて測定する。古典論では、粒子の位置と運動量は全ての時間において確定した値を持っているから、粒子Sの時刻t₀における位置をx₀ 、運動量p₀ をとする。ここで測定したいのは、このx₀とp₀ であるが不完全な観測装置(Ｍ)では、正確に測定することができない。

　このような場合、真の物理量の周りに何らかの確率分布に従って測定値が存在していると考えるのが自然である。

　つまり、位置と運動量の測定値をそれぞれx_M 、p_M とする。そして、観測装置(Ｍ)との相互作用によって位置の測定値にΔx_iのずれが生じる確率をP_iとする。同様に、観測装置(Ｍ)との相互作用によって運動量の測定値にΔp_iのずれが生じる確率をq_iとする。この時、測定値の平均値をそれぞれ<x_M> 、<p_M>とすれば、

　　　　　　　　　　　　　　　　　　　　<x_M>＝ΣP_iΔx_i＋x₀                                 (6.1)

　　　　　　　　　　　　　　　　　　　　<p_M>＝ΣP_iΔp_i＋p₀                                 (6.2)

と表現できる。

　ここで、ε(x)≡<(x_M−x₀)²>^1/2 及び η(x)≡<(p_M−p₀)²>^1/2 を定義すれば、

　　　　　　　　　　　　　　　　　ε(x)≡<(x_M−x₀)²>^1/2＝{ΣP_i(x₀＋Δx_i−x₀)²}^1/2＝(ΣP_iΔx_i²)^1/2＝<Δx²>^1/2　　　(6.3)

　　　　　　　　　　　　　　　　　　　　　　　　　η(p)≡<(p_M−p₀)²>^1/2＝{ΣP_i(p₀＋Δp_i−p₀)²}^1/2＝(ΣP_iΔp_i²)^1/2＝<Δp²>^1/2     　(6.4)

であるが、これは単なる標準偏差である。当然、<Δx²>^1/2≧0　、<Δp²>^1/2≧0なので、何の変哲もない結論ではあるが、位置と運動量の標準偏差をΔx、Δpと表せば象徴的に

　　　　　　　　　　　　　　　　　　　　　　　　　ε(x)η(p)＝ΔxΔp≧0　　　　　　　　　　(6.5)

となる。

　今考えているのは、古典論であるから当然の帰結である。しかし、ここで用いた観測装置(Ｍ)は観測が観測対象に影響を与えるという意味で、ハイゼンベルクの不確定性原理でいう量子的な観測である。たが、以上のように位置と運動量の標準偏差の積の最小値が有限になるという結論を見出すことはできない。そこに、有限な量としてћ/2という値を置くことは、他から導くことができないという意味でやはり原理なのである。前節では、量子力学のファーマリズムからΔxΔp≧ћ/2という関係を導いたが、これをハイゼンベルクの不確定性原理と同定して来たのが小澤不等式以前の物理学である。今回発表された実験結果は、この同定が誤りである可能性が高いことを示すものである。

６．３　量子力学を考慮した位置と運動量の観測

　いよいよ量子力学を考慮に入れて、小澤不等式を導くことにするがここでは前節「５．不確定性原理」までの考察と連続性を保つため、波束の収縮を仮定する。

　さて、量子力学を考慮する場合には、６．２の考察を次のように修正しなければならない。

　　　　�@　観測対象は粒子ではなく、ある系の観測となる。そして、この状態は位置と運動量の固有状態ではないものとする。

　　　　�A　時刻t₀において、観測される系は確定した位置も運動量も有していない。

　まず、系の波動関数をΨ(x,t)と表すことにする。そうすると、時刻t₀で系で観測される物理量の期待値及び標準偏差σは、

　　　　　　　　　　　　　　　<x₀>＝<Ψ(x,t₀)|X|Ψ(x,t₀)>　　　　　　(6.6)

　　　　　　　　　　　　　　　<p₀>＝<Ψ(x,t₀)|P|Ψ(x,t₀)>                        (6.7)

                                                σ（x₀）＝（<x₀²>−<x₀>²）^1/2                                  (6.8)

σ（p₀）＝（<p₀²>−<p₀>²）^1/2                                  (6.9)

である。

また、象徴的に記述すれば、 |σ（x₀）|＝Δx₀、|σ（p₀）|＝Δp₀であり、前節で導いたファーマリズムによる不確定性原理より、

　　　　　　　　　　　　　　　|σ（x₀）||σ（p₀）|＝Δx₀Δp₀≧ћ/2　　　　　　　　　 (6.10)

となる。標準偏差の関係は、量子的な揺らぎ(前節では、「固有状態の重ね合わせの状態から、観測により１つの固有状態に収縮する標準偏差」と説明している)を表すものであり、ハイゼンベルクの不確定性原理とは意味の異なるものである。

　さて、これらの数学的関係から小澤不等式を導くことが可能である。

　まず、式(6.3)より、

　　　　　　　　　　ε²(x)≡<(x_M−x₀)²>＝ΣP_i(x₀＋Δx_i−x₀)²

　　　　　　　　　　　　　　　　　　　＝ΣP_i(x_Mi−x₀)²　　　（x_Mi≡x_M＋Δx_i）

　　　　　　　　　　　　　　　　　　　＝ΣP_ix²_Mi−2x₀x_MiP_i＋x₀²P_i＝<x_M²>−2x₀<x_M>＋x₀²

　　　　　　　　　　　　　　　　　　　＝<x_M²>−<x_M>²＋<x_M>²−2x₀<x_M>＋x₀²

　　　　　　　　　　　　　　　　　　　　　　　　　　　　＝σ²（x_M）＋（<x_M>−x₀）²≧σ²（x_M）

　　　　　　　　　　　　　　　∴ε(x)≧σ（x_M）

となる。なお、ここでx₀は確定しておらず仮想的な量である。

　同様にη(p)についても計算すると、

　　　　　　　　　　　　　　                　    ε(x)≧σ（x_M）                          　　　 (6.11)
　　　　　　　　　　　　　　　　　                    η(p)≧σ（p_M）                            　　　 (6.12)

となる。

　さて、ここでx_M−x₀＝u　、p_M−p₀＝vとおけば、σ（x_M）＝σ（u＋x₀）、σ（p_M）＝σ（v＋p₀）であるが、この取扱いが古典論の場合と量子論の場合との本質的な違いとなる。古典論の場合は、x₀とp₀は確定した値を持っているため、σ（x₀）＝0、σ（p₀）＝0 となり、
σ（x_M）＝σ（u）、σ（p_M）＝σ（v）で、式(6.3)式(6.4)に相当する。しかし、量子論の場合はx₀とp₀は値が確定しておらず、式(6.8)式(6.9)のように分散を有している。

　すると、観測装置(Ｍ)による確率分布と量子的な揺らぎによる確率分布は独立であるから、分散の公式を用いて

　　　　　　　　                 σ²（x_M）＝σ²（u＋x₀）＝σ²（u）＋σ²（x₀）　　　　　　　　 　 (6.13)
　　　　　　　　　            　 σ²（p_M）＝σ²（v＋p₀）＝σ²（v）＋σ²（p₀）　　　　　　　　   　(6.14)

が成り立つ。

　ここで、 式(6.13)と式(6.14)からσ（x_M）σ（p_M）を求めると、

　　　　　　　　　　　　σ（x_M）σ（p_M ）＝σ（u）σ（v）＋σ（u）σ（x₀）＋σ（v）σ（p₀）＋σ（x₀）σ（p₀）    　　　　　　　　(6.15)

となるが、σ（x_M）σ（p_M ）という量を考えてみると、これは観測装置(Ｍ)によって示される値であるから、古典的な量と考えることができ、σ（x_M）σ（p_M ）≧0である。（σ（x_M）＝<x_M²>−<x_M>²で　σ（x_M）＝<x_M²>−<x₀>²ではないことに注意)

古典的計器の最も観測精度が高い場合にはσ（x_M）σ（p_M ）＝0であるため、式(6.15)を

　　　　　　　　　　　　　σ（u）σ（v）＋σ（u）σ（x₀）＋σ（v）σ（p₀）＋σ（x₀）σ（p₀）＝0　　　　　　　　　　　　(6.16)

とする。

　さて、標準偏差は0以上であるから式(6.16)が成り立つためには、通常の場合なら全ての項が0になる必要がある。

しかし、σ（x₀）σ（p₀）＝0が成り立つことは、式(6.10)に反する。矛盾が生じるということは、これまでのロジックのどこかに欠陥があることを意味しており、どこに原因があるのかあれこれと試行錯誤したところ、式(6.13)と式(6.14)を虚数を用いて次のように変更すれば良いことがわかる。

　　　　　　　　　　　　　　　σ²（x_M）≡σ（x_M）σ（x_M）^*＝（σ（u）＋iσ（x₀））（σ（u）−iσ（x₀））　                          

                                                σ²（p_M）≡σ（p_M）σ（p_M）^*＝（σ（v）＋iσ（p₀））（σ（v）−iσ（p₀））　                          

                                        ∴σ（x_M）＝σ（u）＋iσ（x₀）                                    (6.17)
　　　　　　　　　　　　　　　　　　　　　　                　 ∴σ（p_M）＝σ（v）＋iσ（p₀）　                                 (6.18)

　式(6.17)と式(6.18)の意味については、詳細に検討しなければならないが、とにかく式(6.16)のようにしてσ（x_M）σ（p_M）を求めてみると、

　　　　　　　　　　　　　　　　　　　　　　σ（x_M）σ（p_M）＝σ（u）σ（v）−σ（x₀）σ（p₀）＋iσ（x₀）σ（v）＋iσ（u）σ（p₀）＝0 　　　　　(6.19)

となる。ここで、σ（x₀）σ（p₀）を右辺に移し絶対値取ると、

　　　　　　　　　　　　　　　|σ（u）σ（v）＋iσ（x₀）σ（v）＋iσ（u）σ（p₀）|

　　　　　　　　　　　　　　＝{σ²（u）σ²（v）＋（σ（x₀）σ（v）＋σ（u）σ（p₀））²}^1/2 ＝|σ（x₀）σ（p₀）|＝|σ（x₀）||σ（p₀）|

さらに、三角不等式を２度適用すると、左辺は、

　　　　　　{σ²（u）σ²（v）＋（σ（x₀）σ（v）＋σ（u）σ（p₀））²}^1/2≦|σ（u）σ（v）|＋|σ（x₀）σ（v）＋σ（u）σ（p₀）|

　　　                                           ≦|σ（u）σ（v）|＋|σ（x₀）σ（v）|＋|σ（u）σ（p₀）|

　　　　　　　　　　　　　　　　　　　　　　　　 ＝|σ（u）||σ（v）|＋|σ（x₀）||σ（v）|＋|σ（u）||σ（p₀）|

となるため、

　　　　　　　　　　　　　　　　　　|σ（u）||σ（v）|＋|σ（x₀）||σ（v）|＋|σ（u）||σ（p₀）|≧|σ（x₀）||σ（p₀）|

である。そして、σ（u），σ（v），σ（x₀），σ（p₀）はすべて実数であるため、|σ（u）|＝σ（u）等が成り立ち左辺を置き換え、式(6.10)を適用すると、

　　　　　　　　　　　　　σ（u）σ（v）＋σ（v）σ（x₀）＋σ（u）σ（p₀））≧|σ（x₀）||σ（p₀）|≧ћ/2　　　　　　　　　　　　 (6.20)

となる。

　　また、式(6.3)より、

　　　　　　　　　　ε²(x)＝<(x_M−x₀)²>＝<u²>≧<u²>−<u>²＝σ²（u）                  ∴ε(x)≧σ（u）　　　　　(6.21)

であり、式(6.4)より、

　　　　　　　　　　　　　η²(p)＝<(p_M−p₀)²>＝<v²>≧<v²>−<v>²＝σ²（v）                 ∴η(p)≧σ（v）　  　　　(6.22)

となる。この式(6.21)と式(6.22)を式(6.20)に代入すれば、

　　　　　　　　　　　　　　ε(x)η(x)＋η(p)σ（x₀）＋ε(x)σ(p₀）≧|σ（x₀）||σ（p₀）|≧ћ/2　　　　　　　　　　　　　　　 (6.23)

であり、

　　　　　　　　　　ε(x)η(x)＋η(p)σ（x₀）＋ε(x)σ(p₀）≧ћ/2　　　　　　　　　　　　　　　　　　　　　　　　　　 (6.24)

となり、小澤不等式を導くことができる。

　さて、式(6.17)及び式(6.18)の意味をあれこれ考えてみたが、今のところ判然としない。そこで、演算子によるアプローチを試みることとする。

　物理量をそれぞれ、u →U、v → V、x₀→X₀ 、p₀→P₀ 、x_m→X_m、p_m→P_mと置き換えれば、

                    　X_m＝U＋X₀　                            P_m＝V＋P₀     　　　　　　　　　　　　　　　　　　　　　 （6.25)             　　　　　

である。ここで、前節の式(5.10)

　　　　　　　　　　ΔAΔB≧｜Im({(Ψ　，[A ，B]Ψ)})｜/2　＝ |[A ，B]| /2　　　　　　　　　　　　　　    (5.10)

をX_mとP_mに適用すれば、

　　　　　　　　　　　　　　　　ΔX_mΔP_m≧｜Im({(Ψ　，[X_m ，P_m]Ψ)})｜/2　　　　　　　　　　　　　　　　　　　　　　　　(6.26)

であるが、観測装置Ｍによって示される物理量はもはや相関することは無いため、[X_m ，P_m]＝0である。(これを、古典的に理想的な観測とみなして、σ（x_M）σ（p_M ）＝0としたのが、式(6.16)である)

　従って、式(6.25)から

　　　　　　　0＝[X_m ，P_m]＝[U ，V]＋[U，P₀]＋[X₀ ，V]＋[X₀ ，P₀]

　　　　　　　　∴[U ，V]＋[U，P₀]＋[X₀ ，V]＝−[X₀ ，P₀]＝−iћ　　　　　　　　　　　　　　　　　　　　　　(6.27)

が成り立つことがわかる。

　さて、ここで式(6.27)について、波動関数Ψにより平均を求めて絶対値を計算すれば、式(6.20)が得られそうなことがわかるが、この波動関数Ψがどういうものなのか明らかにしなければ、式(6.17)や式(6.18)のように「正しい結果が得られるから、このように仮定する。」といった曖昧な論法になってしまう。そこで、観測装置Ｍで生じている過程を考察し、系の状態を明らかにすることが必要となる。

６．４　観測装置Ｍの観測過程

　観測装置Ｍで、観測される直前の観測系の波動関数をΨ(x)はδ関数により、

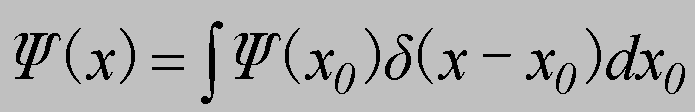　　　　　　　                                     (6.28)

と表すことができる。

　一方で、このような観測系に対して観測装置Ｍが位置を測定するよう構成させているとすれば、観測装置Ｍの量子的部分の波動関数Φはyを用いて式(6.28)と同様に、

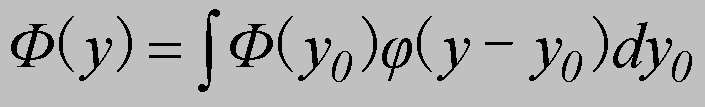　　　　　　　　　　　　                        (6.29)

表わすことができる。なお、式(6.29)がδ関数δ(y-y₀)ではなく、波束φ(y-y₀)による展開となる理由は、実際の観測装置は位置を特定するような理想的な観測をできないことによる。

　さて、フォン・ノイマンの観測理論によると、上記のような観測される系と観測装置の量子的部分が観測のために相互作用すると、結合系は時間発展により、

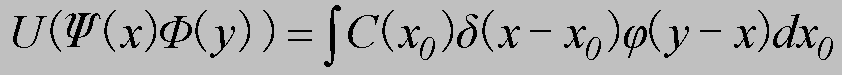　　　　　　　　　　　　      (6.30)

となることが知られている。なお、ここでUは結合系の時間発展のユニタリー演算子を意味する。

さて、式(6.30)のままでは波束の収縮は生じておらず、測定値は確定していない。そのためには、観測系と観測装置Ｍの量子的な部分との結合系を、計器のような古典的な系と相互作用させる必要がある。古典的な系との相互作用として、測定値x_Mが得られたとすると式(6.30)は波束の収縮を起こし、

　　　　　　　　　　　　C(x₀)φ(x_M - x₀)                                               (6.31)

という状態になる。

　なお、式(6.29)のΦ(y₀)について考えてみると、観測装置というのは観測できる範囲内でなら測定値が得られる確率は一定であるのが当たり前である。測定値が得られる確率が異なるのなら、観測装置としての体をなさない。従って、式(6.29)のΦ(y₀)は観測装置Ｍが測定できる範囲では、Φ(y₀)＝１、測定できない範囲内ならΦ(y₀)＝０であると考えられる。そうすると、これはファインマンの観測理論で示されているものではないが、式(6.31)のC(x₀)は恐らく、

　　　　　　　　　　　　C(x₀)≈Ψ(x₀)　　　∴C(x₀)φ(x_M - x₀)≈Ψ(x₀)φ(x_M - x₀)　　　　　 (6.32)

となることが予想される。こうすると式(6.32)は、x₀を中心とした波束に波動関数が収縮し、その波束の中にあるx_Mを観測したものが測定値として示されるを表しており、本来x₀という位置が測定されるはずのものが測定誤差によりx_Mとなり、同時に運動量についても擾乱を起こすことを意味する。この運動量の擾乱とは、x₀を中心とした波束の運動量p₀からずれた測定値p_Mが得られることである。例えば、波束の収縮が瞬時に起きたと仮定すれば、p_M≈p₀＋(x_M−x₀)m/��tとなるであろう。(ただし、我々はx₀もp₀も正確にはわからない。なお、波束の中で観測される位置や運動量は、ボーム力学を用いるとわかりやすい。http://physics.nomaki.jp/borm14.html)　

　さて、このような式(6.32)を

　　　　　　　　　　　　C(x₀)φ(x_M - x₀)≈Ψ(x₀)φ(x_M - x₀)＝Ψ(x₀)φ(u)≡｜x₀  ，u＞

として、式(6.27)の平均求めてみると、

　　　　　　　　　　＜x₀  ，u｜　[U ，V]＋[U，P₀]＋[X₀ ，V]｜x₀  ，u＞＝−iћ　　

　　　　　　　　　∴＜｜[U ，V]｜＞＋＜｜[U，P₀]｜＞＋＜｜[X₀ ，V]｜＞＝−iћ　　

ここで、両辺の絶対値を取ると、

　　　　　　　　　｜＜｜[U ，V]｜＞＋＜｜[U，P₀]｜＞＋＜｜[X₀ ，V]｜＞｜＝ћ

三角不等式より、

　　　　　　　　　｜＜｜[U ，V]｜＞｜＋｜＜｜[U，P₀]｜＞｜＋｜＜｜[X₀ ，V]｜＞｜≧ћ

となる。ここで式(5.10)から、標準偏差を用いると、

　　　　　　　　　  2{σ（u）σ（v）＋σ（v）σ（x₀）＋σ（u）σ（p₀）}≧ћ

　　　　　　　　　　　　   　∴σ（u）σ（v）＋σ（v）σ（x₀）＋σ（u）σ（p₀）≧ћ/2

となり、再び式(6.20)を導出することができる。

これにより、式(6.17)や式(6.18)のような意味不明な仮定を置かず、小澤不等式が導出できる。

量子力学に戻る　

ＴＯＰページに戻る

前に戻る　次に進む

ｱﾏﾁｭｱﾘｽﾞﾑの量子力学