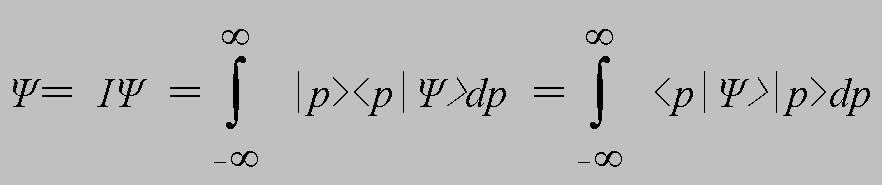量子力学の基礎概念

　前節では、時間推進演算子を求めたが、同様にして空間推進の演算子を求めることができる。

ある波動関数をφ(x,y,z)とする。空間は３次元であるため、それぞれの座標についての推進演算子を考える必要がある。そこで、y方向の座標を+εだけずらすユニタリー演算子をU_y(ε)とする。

　従って、

　　　　　　　　　　　　　　　U_y(ε)φ(x,y,z)＝φ(x,y+ε,z)　　　　　　　　　　　　　　　　　　　　　　　  　　(4.1)

が成り立つ。

さて、前節の(3.15)より、　H＝(-i)lim_(ε→0)(U (ε)−1)／ε＝(-i)lim_(ε→0)(exp(iεH)−1)／ε が成り立っており、このハミルトニアンであるHが時間推進演算子の生成子であったが、同様にしてy方向の空間推進演算子の生成子K_yを求めることとする。

つまり、

　　　　　　　　　　　　　　　　　　　　　　K_yφ(x,y,z)＝(-i)lim_(ε→0)(U_y (ε)−1)φ(x,y,z)／ε＝(-i)lim_(ε→0))(φ(x,y+ε,z)−φ(x,y,z))／ε

である。そして、lim_(ε→0))(φ(x,y+ε,z)−φ(x,y,z))／εは、yについての偏微分であるから、

　　　　　　　　　　　　　　　　　　　　　　K_yφ(x,y,z)＝(-i)∂φ(x,y,z)／∂y                                                      

となる。同様にして、

　　　　　　　　　　　　　　　　　　　　　　K_xφ(x,y,z)＝(-i)∂φ(x,y,z)／∂x    

                                                K_zφ(x,y,z)＝(-i)∂φ(x,y,z)／∂z    

であり、ベクトルを用いると、

　　　　　　　　　　　　　　　　　　　　　 K＝(-i)(∂/∂x,∂/∂y,∂/∂z)＝(-i)∇　　　　　　　　　　　　　　(4.2)

となる。これが、空間推進演算子の生成子であり、空間推進演算子は、

　　　　　　　　　　　　　　　U(ε)＝exp(ir･K)    （r＝(x,y,z)）　　　　　　 　　　　   (4.3)

である。

　さて、見てのとおり(4.2)にћを乗じれば、これはまさしく運動量演算子である。ここでは、原子単位系を用いているため、ћ＝１であり、運動量演算子P＝Kとすることができる。天下り的に、P⇒(-i)∇と変換してシュレディンガー方程式を立て解を求めるのが通常であるが、そのことにはこのような背景がある。

　ところで、この節では抽象的な状態ではなく、敢えてφ(x,y,z)という座標表示を用いて説明している。これは、運動量演算子を敢えて座標表示で求めることにより、通常シュレディンガー方程式を立てる際に利用するP⇒(-i)∇という変換に対比させ、求まった空間推進演算子の生成子が、運動量演算子と同等であることを示すためである。逆にいえば、運動量演算子が(4.2)のような形式となるのは、状態を座標表示として、つまり波動関数として表した場合に限定され、別の表示を用いれば演算子が違った形式になると考えられる。そこで、座標表示に対して、運動量表示というものを考えてみることとする。

　考察を単純にするため、１次元についてのみ考えることとする。運動量演算子をPとすれば、その固有状態|p>に対しては、

　　　　　　　　　　　　　　　P|p>＝p|p>　　　　                                     (4.4)

が成り立つ。これに座標表示を与えれば、

　　　　　　　　　　　　　　　　　　　　　 P<x|p>＝p<x|p>＝P^(x)<x|p>      (P^(x)= -i∂/∂x )            (4.5)

となる。 Pが座標表示に作用する演算子であることを表すために、P= -i∂/∂x の場合には、P^(x)=-i∂/∂xと表すことした。

さて、(4.5)の解は簡単に求めることができ、<x|p>∝exp(ixp)となることがわかる。（なお、このことは、運動量の固有状態の波動関数は、k=pの波数をもつ平面波であることを示しており、ド・プロイの描像と合致する。）また、(4.4)にp'の運動量表示を与えるなと、

　　　　　　　　　　　　　　 P<p'|p>＝p<p'|p>                                         (4.6)

となり、第２節で座標表示で用いた(2.9)　<x'|x>＝δ（x'−x）と対比すれば、

　　　　　　　　　　　　　　　　　　　　 <p'|p>＝δ（p'−p）                                                                                   (4.7) 

であることがわかる。また、(2.7)と同様に、任意の状態Ψを同じように運動量表示の展開により、

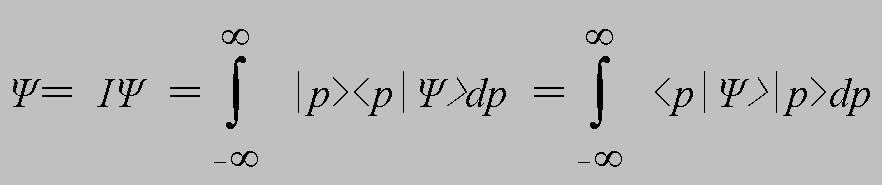                                                          (4.8)

と表すこともできる。さて、(2.7)と(4.8)は同じ任意の状態Ψを、ぞれぞれ座標表示と運動量表示で展開したものであるから、

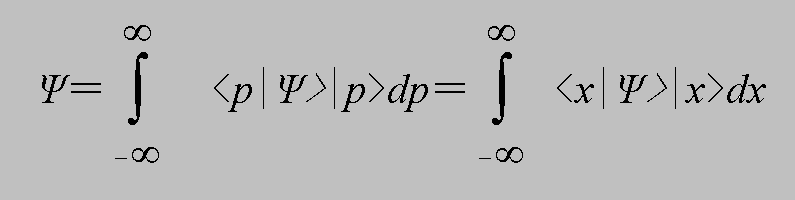                                                         (4.9)

とすることもできる。そして、この状態Ψにx'で表示を与えると、

                                              (4.10)

となる。（cを定数とし、<x|p>∝exp(ixp)を用いている。Ψ（p）は状態Ψの運動量表示である。）

さて、c=(2π)^-1/2、<x|p>＝(2π)^-1/2exp(ixp)とすると、（4.10)はフーリエー変換そのものであることがわかる。つまり、任意の状態について、運動量表示から座標表示の変換はフリーエー変換により行われるのである。そして、フーリエー変換の定義より、逆に座標表示から運動量表示に変換する場合は、その逆フーリエー変換によって行われる。

また、このことから運動量演算子の表示形式の変換についても、考えることができる。（4.10)にP^(x')=-i∂/∂x'を作用させてみると、

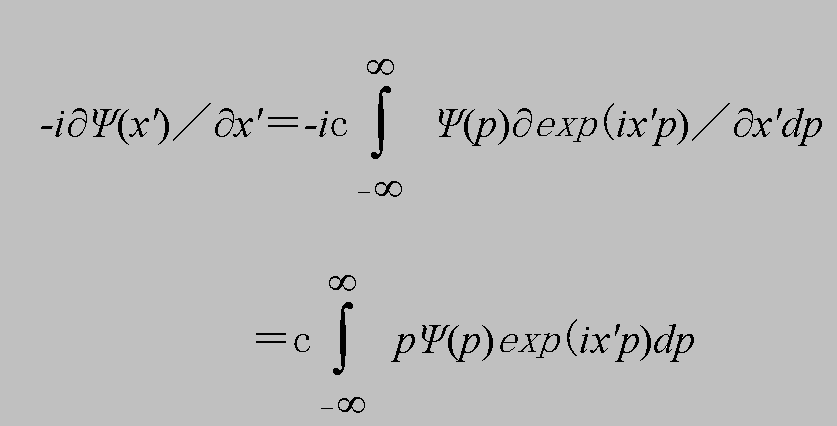                                                  (4.11)

となる。わかりやすくするため、逆変換で表すと、

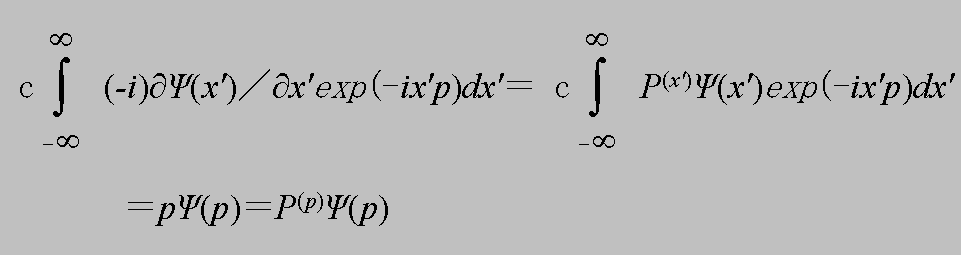                                 (4.12)

となる。つまり、座標表示の状態に作用する運動量演算子はP^(x)=-i∂/∂xあるが、運動量表示の状態に作用する運動量演算子はP^(p))=pとなることがわかる。このことは、位置の演算子Xについても同様なことがいえ、座標表示の状態に対しては、X^(x)＝xである。これを(4.11)同様にーリエー変換を行うと、

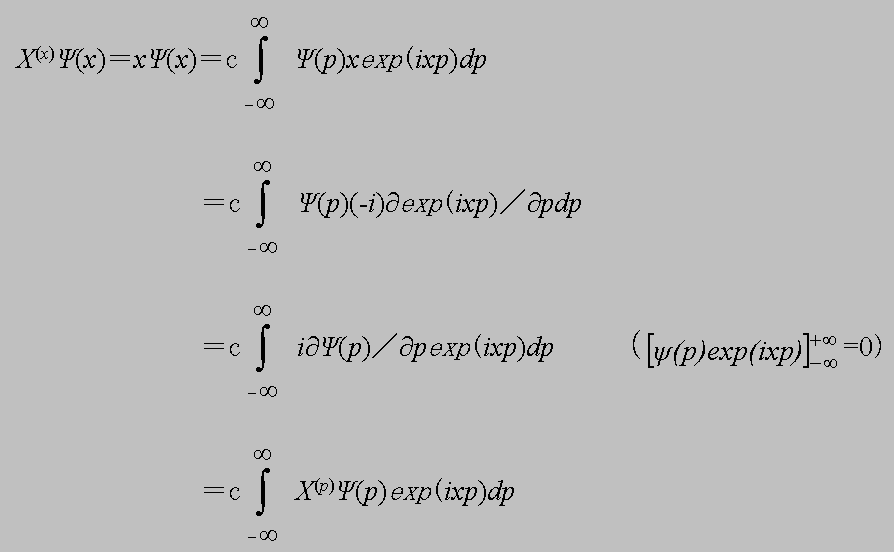                               (4.13)

となり、運動量表示の状態に作用する位置の演算子はX^(p)＝i∂／∂pであることがわかる。

位置の演算子と運動量演算子の関係をまとめると、次のようになる。

　なお、上記のことは３次元でも本質的に変わらない。この場合、c=(2π)^-3/2、X^(p)＝i（∂／∂p_x,∂／∂p_y,∂／∂p_z)、exp(ixp)⇒exp(ir･p)とすればよく、フーリエー変換は３次元について行えばよい。

量子力学に戻る　

ＴＯＰページに戻る

前に戻る　次に進む

ｱﾏﾁｭｱﾘｽﾞﾑの量子力学