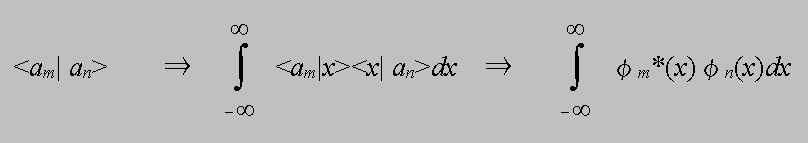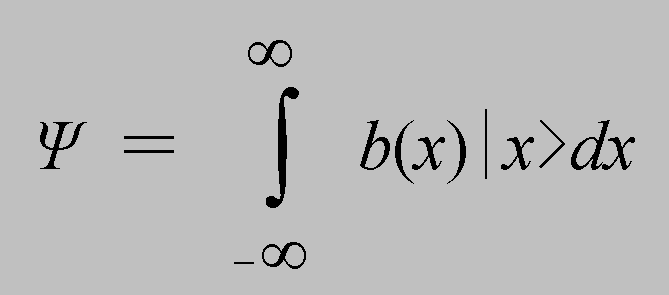 (2.5)
(2.5)
量子力学の基礎概念
2.位置の観測と位置表示
状態は、自己共役線形演算子であるオブザーバブルAの固有関数が張る完全規格化直交関数系|an>により、それぞれの固有状態の重ね合わせとして、次のように一般的に展開される。
Ψ=Σcn|an> (cn= <an|Ψ> A|an>=an|an>) (2.1)
このことは、オブザーバブルすべてに成り立つものと考えているが、位置というオブザーバブルについて、(2.1)の形式が成り立ち得るのか考察するのが、本節の課題である。
まず、一般的な観測の演算子を考えてみる。Ψという状態で理想的な観測を行い、amという観測値を得る過程を演算子Pamで表すととすれば、PamΨ=cm|am>を満たすようなものであろう。従って、
Pam=
|am><am| (2.2)と考えるのが妥当であろう。(なお、これによりAはA=Σan|an><an| =ΣanPanとなり、いわゆるスペクトル分解として表すことができ、観測の演算子 Pamは|am>状態への射影演算子と同じものである。さらに、オブザーバブルは固有状態への射影×固有値となっており、||PamΨ/Ψ
||2を Pamの大きさと定義すれば、確率の測度×固有値という構成になっていることがわかる。)さて、考察を簡単にするため、1次元のみでの位置の観測を考えることにする。(2.1)の形式をそのまま適用すれば、状態は位置固有状態の重ね合わせとして、
Ψ=Σcn|xn>=Σ|xn><xn|Ψ> (X|xn>=xn|xn>) (2.3)
と表記できる。
そして、このような状態Ψに対して理想的な観測を行い、xmという観測値を得る演算子Pxmを作用させれば、
PxmΨ=
|xm><xm|Ψ> (2.4)となるはずである。しかし、位置xnは連続な値を取るので、 このままでは適用できず、xnとxmを連続値をして扱う必要がある。そこで、xn⇒εn と無限小正数εを用いて(2.3)を表してみる。つまり、無限小の大きさに座標を分割し、εnとε(n+1)の間に粒子がある状態を考えてみる。そうすると、(2.3)は
Ψ=Σcn|xn>=Σcn
(εn) |εn >=Σcn/εn |εn > εn=Σbn(εn) |εn > εn (bn=cn /εn)となる。これは、そのまま積分で表すことが可能でき、
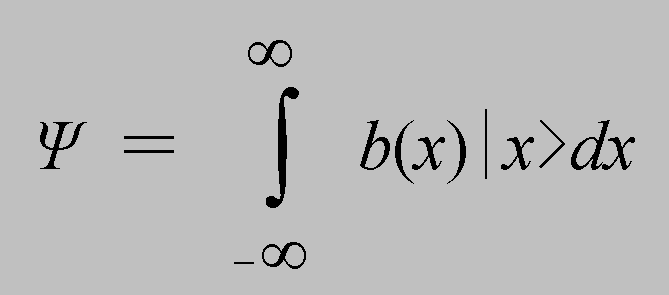 (2.5)
(2.5)
となる。さて、次にPxmを全てのmについて和を取ることを考える。これはすべての射影演算子についての和であるから、恒等演算子Iになるが、これも同じく積分で表すと、
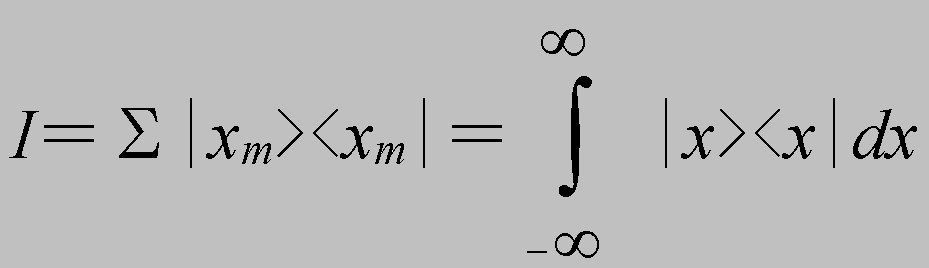 (2.6)
(2.6)
となる。さて、これは恒等演算子であるから、これをΨに作用させても結果はΨとなるので、
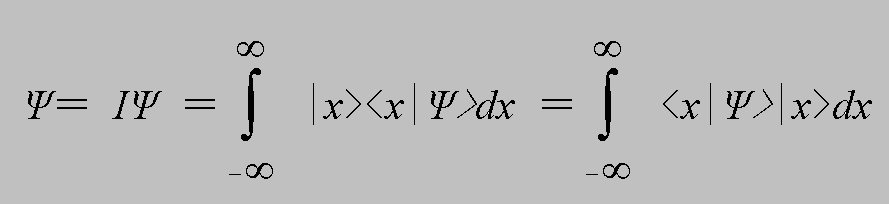 (2.7)
(2.7)
となる。(2.7)と(2.5)を見比べれば、b
(x)=<x|Ψ>となることがわかるであろう。 さて、これまで抽象的なディラックの記法を用いて状態を表示してきたが、<x|Ψ>はこういう状態に表示を与えることを意味している。つまり、Ψ(x)=<x|Ψ>であり、これはxの関数として与えられた状態、つまり波動関数を意味している。同様にして、(2.1)について<x|を作用させると、<x|Ψ>=Σcn<x|an>となり、左辺は波動関数であり、右辺はxの関数としての完全規格化直交関数(φn(x))を表しており、良く見慣れたΨ(x)=Σcnφn(x)となる。このように(2.7)についてを<x'|を作用させると
となるが、(2.8)の関係を満たす<x'|x>は、明らかにδ(x'−x)である。
<x'|x>=δ(x'−x) (2.9)
(2.9)は、位置xの固有状態|x>にx'の表示を与えれば、δ(x'−x)となることを示している。このことは、次のような直観な結論と一致する。
状態ΨにPxを作用させることは、位置xを観測する過程を示しており、PxΨ=|x><x|Ψ>=Ψ(x)|x>となる。これを(2.1)と対比させてみると、cn=Ψ(x)、|an>=|x>である。さらに、前節の定義4より、|an>はΨという状態で理想的な観測を行い、an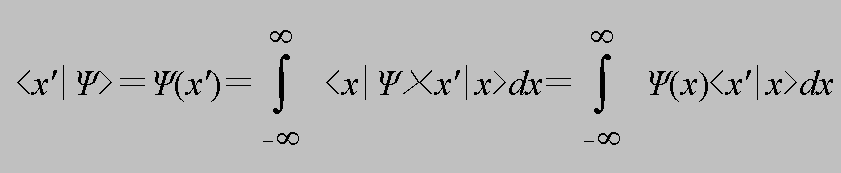 (2.8)
(2.8)
さらに、cn=Ψ(x)ということは、「cncn*の確率で観測値anが得られる。」という前節の定義4より、Ψ(x)Ψ(x)*の確率で観測値xを得られるということになる。これは、波動関数に対する「コペンハーゲン解釈」に一致する結論である。つまり、前節で与えた抽象的な形式は、「コペンハーゲン解釈」とも整合するものである。
さて、状態に表示を与えるということは、抽象化したものをわざわざ具体的ものに戻すことであり、これ自体はあまり意味のあることではない。しかし、理解を助け見通しをよくするという長所がある。そこで、抽象的なディラックの表記に表示を与える。
Ψ=Σcn|an> ⇒ <x|Ψ>=Σcn<x|an> ⇒ Ψ(x)=Σcnφn(x) (Aφn(x)=anφn(x))