(1.61)
�{�[���͊w
�P�D7�@�����ԂP
�P�D�V�D�P�@�����ԂƂ́H
�@�P.�S�߂Ŕ����Ԃ̗�Ƃ��ăK�E�X�g���������A���̉��p�Ƃ��ĂP.�T�ߋy�тP.�U�߂ł��̉��p�Ƃ��ē�d�X���b�g�̃V�~�����[�V�������s�������A�{�߂ł͈�ʓI�Ȕ����Ԃɂ��čl�@����B
�@��ʓI�ɔ�������(r,t)�́A���鎞�Ԃ�z�Ɋ܂܂Ȃ��n�~���g�j�A��(�g)�̌ŗL��(��n(r))����āA
�@�@�@�@�@�@�@�@�@�@�@�@��(r,t)����an��nexp(-iEnt)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.60)
�ƕ\�����B�����ŁA����nr���Ęa�ł���Aan�͔C�ӂ̕��f���ł���B�܂��A�g��n��En��n�����藧�B�Ȃ��A�g�����Ԃ�z�Ɋ܂ޏꍇ�ɂ�an�͎��Ԉˑ��������A�ۓ��_�̏o���_�ƂȂ�B
���āA���̔�������(r,t)���A��(1.1)��(r,t)��Rexp(iS)�ɓ��Ă͂߂āAan��Anexp(i��n)(An����n�͎���)�Ƃ���A�@
(1.61)
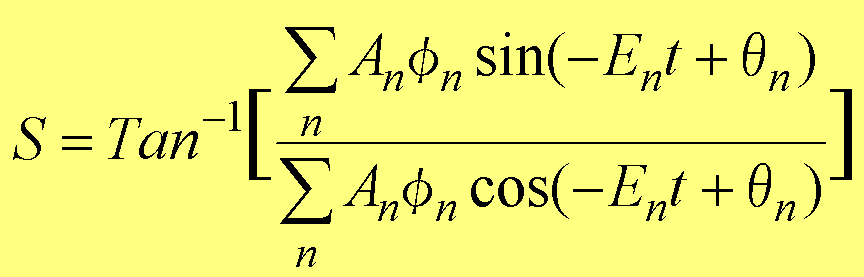 �@�@ (1.62)
�@�@ (1.62)
�ƂȂ�B�܂��A�m�����zP(r,t)�́AP(r,t)��R2���A
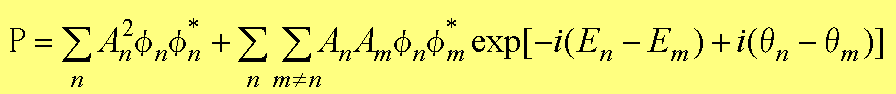 (1.63)
(1.63)
�ł���B��(1.60)�`��(1.63)�ɂ��A�l�@��i�߂Ă������A�����ň����Ă���̂̓G�l���M�[�̔����Ԃł���B
�P�D�V�D�Q�@�����Ԃ̃G�l���M�[
�@��(1.61)���A�����Ԃł͔g�����̐U��R�͎��Ԃ̊��ƂȂ邱�Ƃ��킩��B�����āA��(1.6) �p
���|(1/2m)(��2R �^R) �ɂ��R���狁�߂���ʎq�|�e���V�����p���A���l�Ɏ��Ԃ̊��ƂȂ�B���̂��Ƃ͗��q�̃G�l���M�[-��S/��t�����Ԃɂ���ĕω����A�ۑ�����Ȃ����Ƃ��Ӗ����Ă���A��(1.62)�����Ԃɂ��Δ������A����-��S/��t�����߂Ă݂Ă����炩�ł��낤�B
�@�������A�����Ԃł��G�l���M�[�̕��ϒl�͕ۑ�����邱�Ƃ��A���̂悤�ɂ킩��B
�@�܂��AP(r,t)��R2����A
�@�@�@�@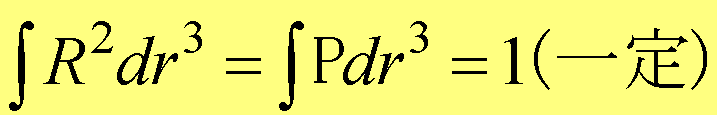 (���̂��Ƃ́A(1.63)��ϕ����Ă��킩��@��An2��1�j
(���̂��Ƃ́A(1.63)��ϕ����Ă��킩��@��An2��1�j
�ƂȂ�B�����āA��(1.8) ��R2�^�݂� �{���E(R2��S�^m)��0 ����A
�@�@�@�@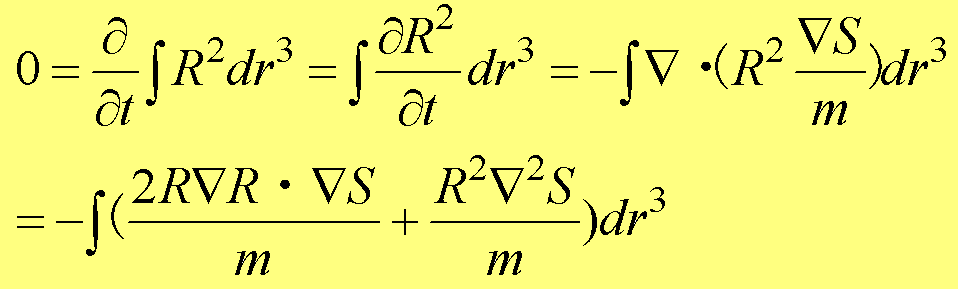
����āA
�@�@�@�@�@ 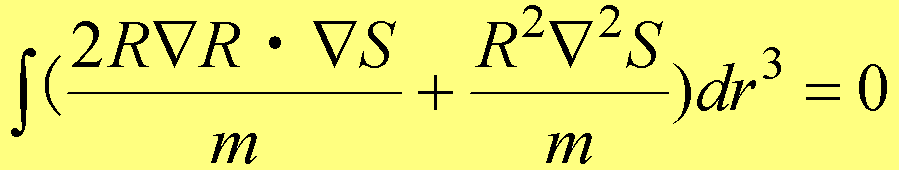 �@�@(1.64)
�@�@(1.64)
�����藧�B
���̎�(1.64)���v�Z�ɗp����ƁA��(1.7)�@��S�^�݂� �{(��S)2�^2m�{�u�{�p ��0�@�ɂ��A
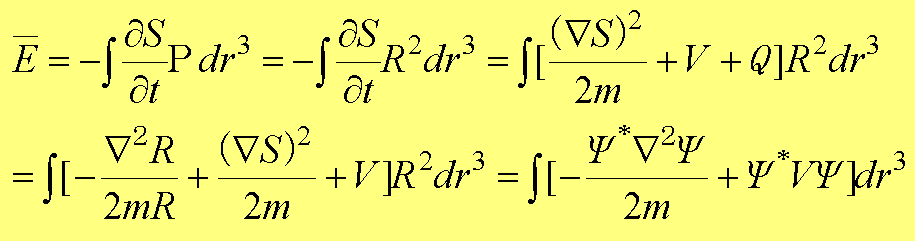 (1.65)
(1.65)
�ƂȂ邱�Ƃ��ȒP�ɂ킩��B
�@��(1.65)�̍Ō�́A�W�����߂ł̃n�~���g�j�A���̕��ϒl�ƑS�������\���ɂȂ�A�G�l���M�[�̕��ϒl���V�����f�B���K�[�������ɂ���ĕۑ�����邱�Ƃ������Ă���B����ɁA�s�m�萫���������������ÓT�Ɍ��ł́A�G�l���M�[���ۑ�����邱�Ƃ�����ɂ�莦�����Ƃ��ł���B
�P�D�V�D�R�@�g�����������̏ꍇ
�@�܂��A�g������������n����n*�̏ꍇ�ɂ��čl�@���Ă݂�B����́A���ɕ����߂�ꂽ���R���q�⒲�a�U���q�̌ŗL��Ԃ̏d�ˍ��킹�ɑ�������B�Ȃ��A�{���I�ȍ��ق��������߁A�ȉ��̋c�_�͈ꎟ���ōs���B
�܂��A(1.62)�����ԂŕΔ������G�l���M�[�����߂Ă݂�ƁA
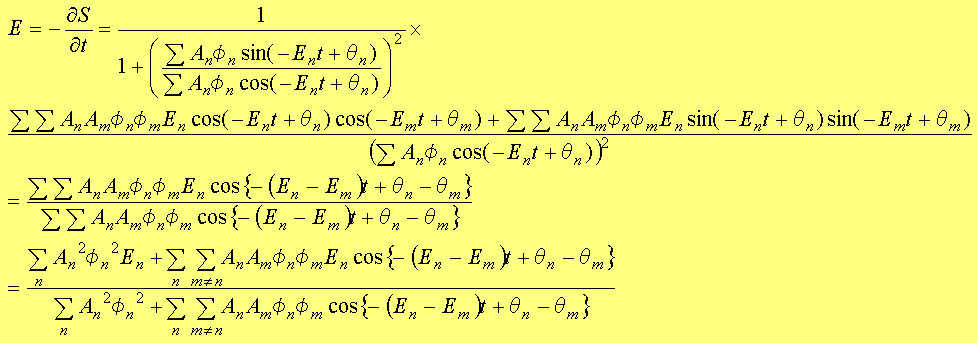 (1.66)
(1.66)
�ƂȂ�B���Ȃ݂ɁA�����R2�ɓ������B
��(1.66)���A�G�l���M�[�͕��σG�l���M�[��An2��n2En�̎���ŐU�����邱�Ƃ��킩��B
���āA1.3�߂ōl�@�����悤�Ɏ������̒���Ԃł́A��S��0�����藧���߁A��(1.7)�@��S�^�݂� �{(��S)2�^2m�{�u�{�p ��0���A
�@�@�@En���|��S�^�݂� ��V�{�pn (�pn���|(1/2m)(��2��n �^��n) )�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(1.67)
�����藧�B������A(1.66)�ɑ������ƁA
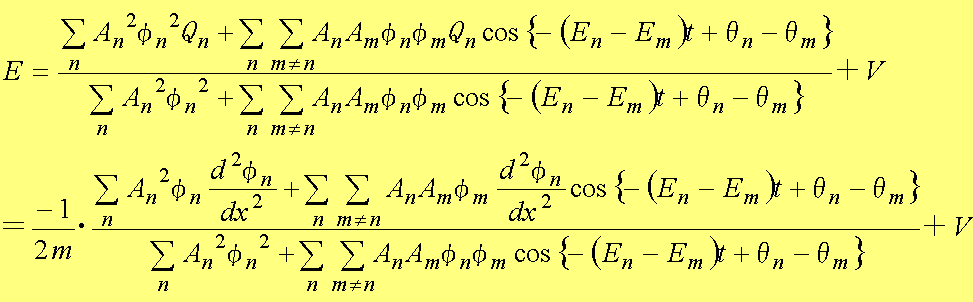 (1.68)
(1.68)
�ƂȂ�B
�@�����āAP����S�ɂ��^���ʂ����߂邽�߁A��(1.62)��Δ���������ƁA
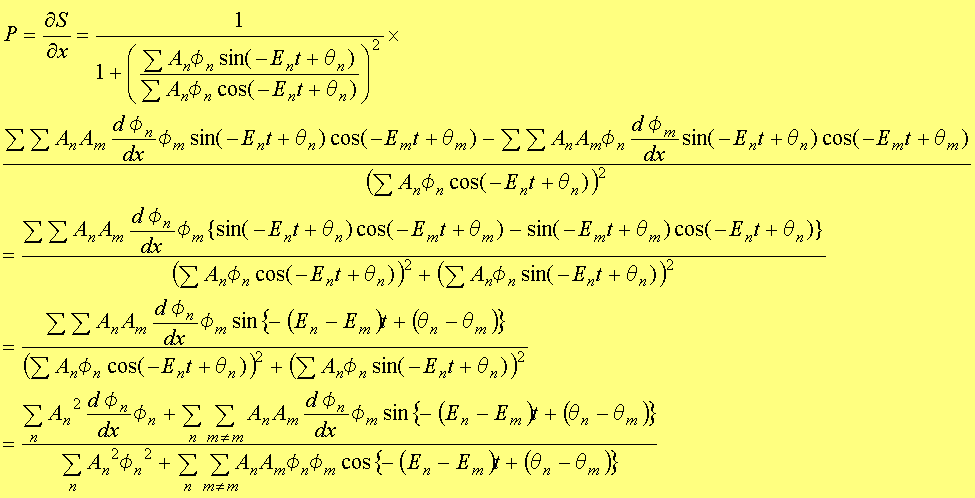 (1.69)
(1.69)
�ƂȂ邱�Ƃ��킩��B�Ȃ��A�����R2�ɓ������B
���̎�(1.69)�́A�����Ԃł͗��q���^���ʂ�L���邱�ƁA�܂�^�����邱�Ƃ��Ӗ����Ă���B����́A���ϓI�ȗ\�z�ƈ�v���錋�_�ł���B
�@��(1.69)�����悵1/2m���悶��ƁA�^���G�l���M�[T�������邪�A��(1.68)�̑�P�������̉^���G�l���M�[T�ň����A�ʎq�|�e���V���������܂�͂��ł���B�������A��(1.69)�̎���̌v�Z�Ƃ����͔̂��ɔώG�Ȃ��̂ƂȂ邱�Ƃ��\�z�����B����ŁA�ʎq�|�e���V�����ڌv�Z����ꍇ���A��(1.61)����̌v�Z�����Ȃ�ώG�ɂȂ���̂Ǝv����B�����ŁA���̎�(1.70)�`��(1.73)�̂悤����(r,t)��\�L���邱�ƂŁA�ʎq�|�e���V�����̌v�Z�����݂邱�ƂƂ���B
�@�@�@�@
��(r,t)����RE�{i��IM�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(1.70)
��RE����An��ncos(-iEnt�{��n)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(1.71)
��IM����An��nsin(-iEnt�{��n)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(1.72)
R��(��RE2�{��IM2)1/2�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@ �@
(1.73)
�܂��A��(1.73)��x�ŕΔ�������ƁA
�@�@�@�@�@�@�@�@�@�@�@��R�^��x��(����RE�^��x�E��RE�{����IM�^��x�E��IM)/R (1.74)
�ƂȂ�B��(1.74)�̕��q�̕Δ������v�Z����ƁA
�@�@�@��{����RE�^��x�E��RE�{����IM�^��x�E��IM}�^��x��{��2��RE�^��x2�E��RE�{��2��TM�^��x2�E��IM�{(����RE�^��x)2+(����IM�^��x)2} (1.75)
�ł���B������Ag(x,t)�Ƃ������Ƃɂ���ƁA
�@�@�@��2R�^��x2��{gR�|(����RE�^��x�E��RE�{����IM�^��x�E��IM)(��R�^��x)}/R2
��{gR�|(����RE�^��x�E��RE�{����IM�^��x�E��IM)2�^R}/R2
��{gR2�|(����RE�^��x�E��RE�{����TM�^��x�E��IM)2}/R3
��{g(��RE2�{��IM2)�|(����RE�^��x�E��RE�{����IM�^��x�E��IM)2}/R3�@�@�@�@�@(1.76)
�ƂȂ�B�����ŁAg(��(1.75))�̑�1���Ƒ�2���́A��(1.76)�̕��q�̌v�Z�ŏ�������邱�Ƃ͂Ȃ�����A
k=��2��RE�^��x2�E��RE�{��2��TM�^��x2�E��IM�Ƃ����ƁA
�@�@��2R�^��x2�̕��q��{k�{(����RE�^��x)2�{(����IM�^��x)2}(��RE2�{��IM2)�|(����RE�^��x�E��RE�{����IM�^��x�E��IM)2
�@�@�@�@��k(��RE2�{��IM2)�{(����RE�^��x)2��RE2�{(����IM�^��x)2��RE2�{(����RE�^��x)2��IM2�{(����IM�^��x)2��IM2
�|(����RE�^��x)2�E��RE2�|(����IM�^��x)2�E��IM2�|2(����RE�^��x)(����IM�^��x)��RE��IM
��k(��RE2�{��IM2)�{(����IM�^��x)2��RE2�{(����RE�^��x)2��IM2�|2(����RE�^��x)(����IM�^��x)��RE��IM
��k(��RE2�{��IM2)�{(����IM�^��x)��RE{(����IM�^��x)��RE�|(����RE�^��x)��IM}�{(����RE�^��x)��IM{(����RE�^��x)��IM�|(����IM�^��x)��RE}
��k(��RE2�{��IM2)�{{(����RE�^��x)��IM�|(����IM�^��x)��RE}{(����RE�^��x)��IM�|(����IM�^��x)��RE}
�@�@�@�@�@��(��2��RE�^��x2�E��RE�{��2��TM�^��x2�E��IM)(��RE2�{��IM2)�{{(����RE�^��x)��IM�|(����IM�^��x)��RE}2
��(��2��RE�^��x2�E��RE�{��2��TM�^��x2�E��IM)R2�{{(����RE�^��x)��IM�|(����IM�^��x)��RE}2�@�@
�@(1.77)
�ƂȂ�B��(1.6) �p ���|(1/2m)(��2R �^R)���A
�@�@�@�p���|(1/2m)[(��2��RE�^��x2�E��RE�{��2��TM�^��x2�E��IM)�^R2�{{(����RE�^��x)��IM�|(����IM�^��x)��RE}2�^R4] (1.78)
�Ɨʎq�|�e���V���������܂�B��(1.71)��(1.72)(1.73)����(1.78)��������ƁA
�@�@�@ �p��E�|V�|(1/2m)P2��(��1.68)�̑�P���|(1/2m)�~(��1.69)�~(��1.69)�@�@�@�@�@�@�@�@�@ (1.79)
�ƂȂ邱�Ƃ��킩��B����́A��(1.7) E���|��S�^�݂��� (��S)2�^2m�{V�{�p �����藧���Ƃ��Ӗ����Ă���B
�@�@��L�̓��e��v��ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�g�����������̌ŗL���ɂ�������
�@�@�G�l���M�[�́A���ԂɈˑ����ω�����B
�A�@��S��0���A���q�͉^�����Ă���B
�B�@ �G�l���M�[�́A���q�̂���ʒu�̗ʎq�|�e���V�����ƌÓT�I�ȃ|�e���V�����Ɨ��q�̉^���G�l���M�[�ł���B
�C�@�@�̎��ԂɈˑ�����G�l���M�[�̕ω��́A�^�����闱�q�̃G�l���M�[�̕ω��ɂ�萶����B
�Ƃ������ƂɂȂ�B�Ȃ��A�����ň����Ă���̂̓|�e���V���������ԓI�ɕω����Ȃ��ꍇ�őJ�ډߒ��ł͂Ȃ��B�]���āA�G�l���M�[���ω�����Ƃ͂����Ă��A���ԂƃG�l���M�[�̕s�m�萫�̊W�ɂ����̂ł���A���ۂɃG�l���M�[���z���E���o����Ă���Ƃ����Ƃ͈قȂ�B�܂��A�G�l���M�[���ϑ����āA��(1.66)�̃G�l���M�[���ϑ�����邱�Ƃ��Ӗ����Ă͂��Ȃ��B���ۂ̊ϑ��ɂ��ẮA�ϑ��̗��_�Ɋ�Â��čl�@�����K�v������B
�@���āA�@�ɂ��ẮA�W�����߂ƈ�v���鎖���ł��邪�A�A�`�C�ɂ��Ă͊T�O�I�ȗ��q�̑��݂����肷�邱�Ƃɂ���Đ����錋�_�ł���B���������A�ʏ�̗ʎq�͊w�̋��ȏ��ł́A�����Ԃ̃G�l���M�[�����ԓI�ɕω����邱�Ƃ͎�����Ă��A���ꂪ�ʒu�ɂ���ĈقȂ�Ƃ������戵�����Ȃ���邱�Ƃ͂قƂ�ǂȂ��B�W�����߂ł͗��q�̑��݂�ے肵�Ă���̂ŁA����������Ă����܂�Ӗ��̖������Ƃ�����ł��낤�B
�@�������A���ݘ_�I���߂ł́A�ʎq�|�e���V�����ƌÓT�I�ȃ|�e���V�����̘a����l�ł͂Ȃ�����(���z�����邱�Ɓj�ɂ�藱�q�̉^���������邽�߁A�G�l���M�[����Ԉˑ�����Ƃ������Ƃ͑傫�ȈӖ������B�����āA���ۂɎ�(1.66)�̃G�l���M�[���ϑ�����邱�Ƃ͖����Ă��A�����Ԃł��m��I�ȃG�l���M�[(���q�̃G�l���M�[)�����݂���Ƃ������Ƃ��A�T�O��͌�����̂ł���B
�@���߂ł́A�ŗL�������f���ɂȂ�ꍇ�ɂ��Ĉ������ƂƂ���B�܂��A�G�l���M�[�̕ω����𐔒l�v�Z�ɂ�苁�߂邱�Ƃ��s���\��ł���B
�����ؽ�т̗ʎq�͊w