(1.61)�Čf��
�{�[���͊w
�P�D8�@�����ԂQ
�P�D�W�D�P�@�g���������f���̏ꍇ
�@�{�߂ł́A�܂��A�g���������f���̔����Ԃɂ��āA�����̏ꍇ�Ɠ��l�Ɏ��̓W�J��i�߂Ă����B
�@��ʓI�ɔ�������(r,t)�́A���鎞�Ԃ�z�Ɋ܂܂Ȃ��n�~���g�j�A��(�g)�̌ŗL��(��n(r))����āA
�@�@�@�@�@�@�@�@�@�@�@�@��(r,t)����an��nexp(-iEnt)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.60) �Čf��
�ƕ\�����B�����ŁA����nr���Ęa�ł���Aan�͔C�ӂ̕��f���ł���B�܂��A�g��n��En��n�����藧�B�Ȃ��A�g�����Ԃ�z�Ɋ܂ޏꍇ�ɂ�an�͎��Ԉˑ��������A�ۓ��_�̏o���_�ƂȂ�B
���āA���̔�������(r,t)���A��(1.1)��(r,t)��Rexp(iS)�ɓ��Ă͂߂āAan��Anexp(i��n)(An����n�͎���)�Ƃ���A�@
(1.61)�Čf��
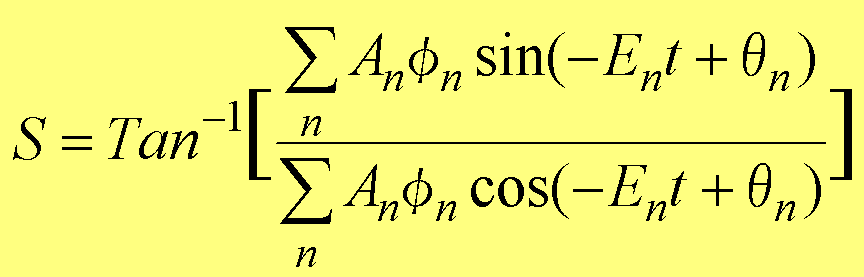 �@�@ (1.62)�Čf��
�@�@ (1.62)�Čf��
�ƂȂ�B�܂��A�m�����zP(r,t)�́AP(r,t)��R2���A
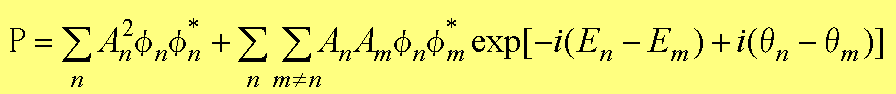 (1.63)�Čf��
(1.63)�Čf��
�ł���B
�@��(1.60)�`��(1.63)�́A�O�߂̓��e���Čf�ڂ������̂ł��邪�A�����������ʂ��̗ǂ����̂ɂ��邽�߁A�e�ŗL�������̂悤�ɒu�������邱�ƂƂ���B�Ȃ��A�{���I�ȈႢ���������߁A�O�ߓ��l�Ɏ��̓W�J�͈ꎟ���ōs�����ƂƂ���B
�@�@�O�߂Ɠ��l�ɁA��(1.60)��an��Anexp(i��n)�Ƃ���A
�@�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@an��n(x)exp(-iEnt)��Anexp(-iEnt�{i��n)��n(x)�@�@�@�@�@�@�@�@�@�@�@�@�@(1.80)
�@�@�����Ŋe�ŗL�����A��n(x)��Rnexp(iS'n)�Ƃ��A��(1.80)�ɑ������ƁA
�@�@�@�@�@�@�@�@�@�@�@�@ an��n(x)exp(-iEnt)��AnRnexp(-iEnt�{i��n�{iS'n) (1.81)
�@�@�ƂȂ�B�Ȃ��A������Rn��S'n�́A�������������x�̊��ł���B
�@�@����ɁA��n�{S'n��Sn(x)�Ƃ���ƁA��(1.81)�́A
�@�@�@�@�@�@�@�@�@�@�@�@ an��n(x)exp(-iEnt)��AnRnexp(-iEnt�{iSn) (1.82)
�@�@�ƂȂ�A��(1.60)�́A
�@�@�@�@�@�@�@�@�@�@�@�@ ��(r,t)����AnRnexp(-iEnt�{iSn) (1.83)
�@�@�ƕ\�����Ƃ��ł���B
�@���̎�(1.83)��p���邱�ƂŁA
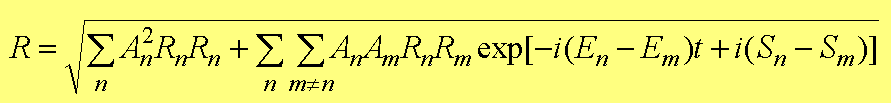 (1.84)
(1.84)
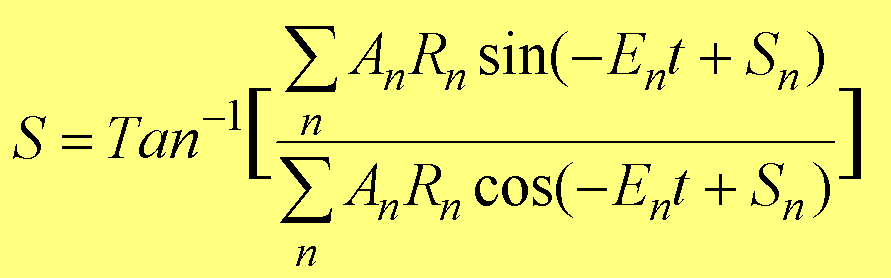 (1.85)
(1.85)
 (1.86)
(1.86)
�@����炩��A�O�߂Ɠ��l�ɂ��ăG�l���M�[�Ɖ^���ʂ����߂�B
�@�܂��A�G�l���M�[�́A��(1.89)�̂悤�ɂȂ�B
�@�@�@�@�@�@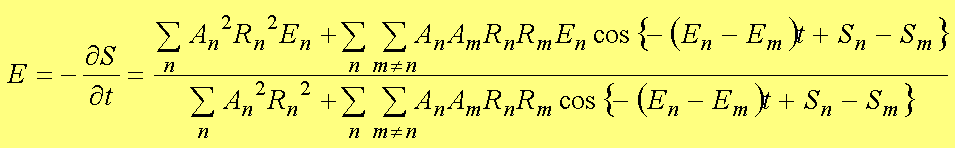 (1.87)
(1.87)
�@�@�@�@�@�@�@�@�Ȃ��A�����ł́A��(1.7)�@��S�^��t �{(��S)2�^2m�{V�{�p ��0���A
�@�@�@�@�@�@�@�@�@�@En���|��S�^��t ��V�{�pn�{(��Sn)2�^2m��V�|(1/2m)(d2Rn �^dx2)�^Rn�{(dSn�^dx)2�^2m �@�@�@ (1.88)
�@�@�@�@�@�ł���B
�܂��A�g=�|(��)2�^2m�{V�@�ł���A�@�g��n(x)���gRnexp(iS'n)��EnRnexp(iS'n)�@�����藧���Ƃ���A
�@En���gRnexp(iS'n)�^Rnexp(iS'n)���|(1�^2m)[(d2Rn �^dx2)�^Rn�{(dSn�^dx)2�{i{2(dRn �^dx)(dSn�^dx)�^Rn�{d2Sn �^dx2}]�{V
�ƂȂ�B�Ȃ��A��n�{S'n��Sn����n�͒萔�ł��邽�߁AdSn�^dx��dS'n�^dx�ł���B
�@�@�@�@�@�������(1.88)�Ɣ�r����ƁA
�@�@�@�@�@�@�@�@�@ 2(dRn �^dx)(dSn�^dx)�^Rn�{d2Sn �^dx2��0�@�@�@�@�@�@�@�@ (1.89)
�����藧�B(�e�ŗL���̃G�l���M�[�ŗL�l�͎���)
�@�����āA�^���ʂ����߂�ƁA��(1.90)�̂悤�ɂȂ�B
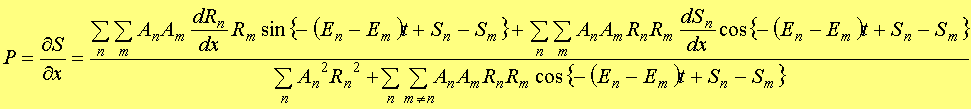 (1.90)
(1.90)
�ƂȂ�B�����āA�ʎq�|�e���V�����p�����߂邪�A����ɂ͑O�߂̎�(1.78)�𗘗p���邱�Ƃ��ł���B
�@�@�p���|(1/2m)[(��2��RE�^��x2�E��RE�{��2��IM�^��x2�E��IM)�^R2�{{(����RE�^��x)��IM�|(����IM�^��x)��RE}2�^R4] �Čf��(1.78)
�@�������A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ��RE����AnRncos(-Ent�{Sn)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(1.91)
��IM����AnRnsin(-Ent�{Sn)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(1.92)
�Ƃ���B
�@ �������ċ��߂��ʎq�|�e���V�������{���ɁA��(1.7)�@��S�^��t�{(��S)2�^2m�{V�{�p ��0�������A���ۂɌv�Z���ċ��߂Ă݂�B
�@�܂��A��2��RE�^��x2�E��RE�{��2��IM�^��x2�E��IM �����߂�ƁA
�@�@�@�@�@�@��2��RE�^��x2�E��RE�{��2��IM�^��x2�E��IM������AnAmRmRn{(d2Rn
�^dx2)Rn�|(dSn�^dx)2}cos{(-(En-Em)t�{Sn-Sm)}
�|����AnAmRmRn{2(dRn
�^dx)(dSn�^dx)�^Rn�{d2Sn
�^dx2}sin{(-(En-Em)t�{Sn-Sm)}
�ł��邪�A��(1.89)����Q����0�ƂȂ�A
�@�@�@�@�@�@��2��RE�^��x2�E��RE�{��2��IM�^��x2�E��IM������AnAmRmRn{(d2Rn �^dx2)Rn�|(dSn�^dx)2}cos{(-(En-Em)t�{Sn-Sm)}
�ł���B����ɁA��(1.88)�y�ю�(1.87)���A
�@�@�@��2��RE�^��x2�E��RE�{��2��IM�^��x2�E��IM���|2m����AnAmRmRn(En-V)cos{(-(En-Em)t�{Sn-Sm)}���|2mER2�{2mVR2 (1.93)
�ƂȂ�B�Ȃ��AR2����RE2�{��IM2������AnAmRmRncos{(-(En-Em)t�{Sn-Sm)}�ł���A��(1.87)�̕����R2�ɓ������B
�@�����āA(����RE�^��x)��IM�|(����IM�^��x)��RE �����߂�ƁA
(����RE�^��x)��IM�|(����IM�^��x)��RE������AnAm(dRn
�^dx)Rmsin{(-(En-Em)t�{Sn-Sm)}
�{����AnAmRmRn(dSn�^dx)cos{(-(En-Em)t�{Sn-Sm)}
�ł��邪�A��(1.90)���A
�@�@�@�@�@ (����RE�^��x)��IM�|(����IM�^��x)��RE��PR2 (1.94)
�ƂȂ�B�Ȃ��AR2����RE2�{��IM2������AnAmRmRncos{(-(En-Em)t�{Sn-Sm)}�ł���A��(1.90)�̕����R2�ɓ������B
����āA��(1.93)�y�ю�(1.94)����(1.78)�ɑ������ƁA
�@�@�@�@�@�@ �p���|(1/2m)[(��2��RE�^��x2�E��RE�{��2��IM�^��x2�E��IM)�^R2�{{(����RE�^��x)��IM�|(����IM�^��x)��RE}2�^R4]
�@�@�@�@�@�@�@�@ ���|(1/2m)(�|2mER2�{2mVR2 )�^R2�|(1/2m)(PR2)2�^R4��E�|V�| P2/2m��E�|V�| (��S)2/2m
�ƂȂ�A��������ƁA
�@�@�@�@�@�@�@E���|��S�^��t ��V�{�p�{(��S)2�^2m
�ł���A��(1.7)�@��S�^��t �{(��S)2�^2m�{V�{�p ��0�@�����藧���Ă��邱�Ƃ��킩��B
��L�̓��e��v��ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�g���������f���̌ŗL���ɂ�������
�@�@�G�l���M�[�́A���ԂɈˑ����ω�����B
�A�@��S��0���A���q�͉^�����Ă���B
�B�@ �G�l���M�[�́A���q�̂���ʒu�̗ʎq�|�e���V�����ƌÓT�I�ȃ|�e���V�����Ɨ��q�̉^���G�l���M�[�ł���B
�C�@�@�̎��ԂɈˑ�����G�l���M�[�̕ω��́A�^�����闱�q�̃G�l���M�[�̕ω��ɂ�萶����B
�ł���A�����̌ŗL���̏ꍇ�Ɠ��l�̌��_�ɂȂ�B
�P�D�W�D�R�@�����Ԃ̃V�~�����[�V����
�@�����Ԃ̃V�~�����[�V�������s���Ă݂邪�A���̍ۂɂ̓��f�����ǂ̂悤�ɑI�����邩���d�v�ƂȂ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��(r,t)����an��nexp(-iEnt)�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.60)
��(1.60)�́At��0�ɂ�����S�Ă�an�����肷��A���̌�̔C�ӂ̎��Ԃɂ�������(r,t)�͂����肳��邱�Ƃ������Ă���B�������A�������
�@�@�@�@�@�@�@�@�@�@�@�@�@��(r,0)����an��n�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ (1.95)
�Ƃ����̂́A��n�����S�������n���`�����邽�߁A�قƂ�ǂ��������\�L���邱�Ƃ��\�ł���ƍl������B���̂��Ƃ́At��0�̏�����ԂƂ��ĔC�ӂ̊���I���ł��邱�Ƃ��Ӗ����Ă��邪�A�����I�ɗL�蓾�Ȃ��悤�ȏ�����Ԃ�ݒ肵�A���ԓI�Ȕ��W���v�Z���Ă��A���܂�Ӗ��������ł��낤�B
�@�����ł܂��́A������Ԃ��K�E�X�g���ł���ꍇ�ɂ��ăV�~�����[�V�������s���Ă݂�B�K�E�X�g���́A���q��������x�Ǐ��I�Ȉʒu�Ɋϑ���������̔g������\���Ă���ƍl���邱�Ƃ��ł��A���̌�A�Ⴆ�P�������^�|�e���V�����⒲�a�U���̃|�e���V�����ɑ��������ꍇ�̔g�������v�Z���邱�Ƃ��\�ł���A�{�[���͊w�ł͂������痱�q�̋O��(�������A�B��̋O�Ղł͂Ȃ�)�₻�̃G�l���M�[�Ƃ��������̂��v�Z���邱�Ƃ��ł���B
�P.�W.�S�@�K�E�X�g���ƂP�������^�|�e���V�����̃V�~�����[�V����
�@������Ԃ���(x,0)��(����x)-1/4exp{-x2/(2��x)}�Ƃ����K�E�X�g���ł���A���̌�ɔ����Ԃ�-a��x��a�͈̔͂ɗ��q���������ꂽ�P�������^�|�e���V�����ɂ��ăV�~�����[�V�������s���Ă݂�B�܂�A����t=0��x��0�ɐ��x��x�����q�𗱎q���ϑ����A���̌�̎��Ԕ��W���V�~�����[�V��������Ƃ������̂ł���B
�@�܂��A�P�������^�|�e���V�����̒������n(x)�́A
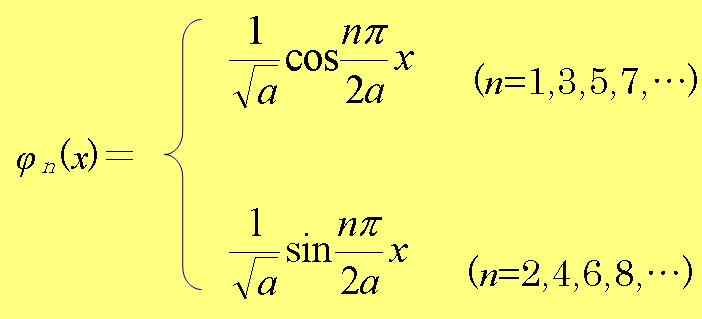 �@�@(1.96)
�@�@(1.96)
�ł���B�܂��A��n(x)�����S�������n�邱�Ƃ���A��(x,0)����An��n�@�Ƃ�An�����߂�ƁA
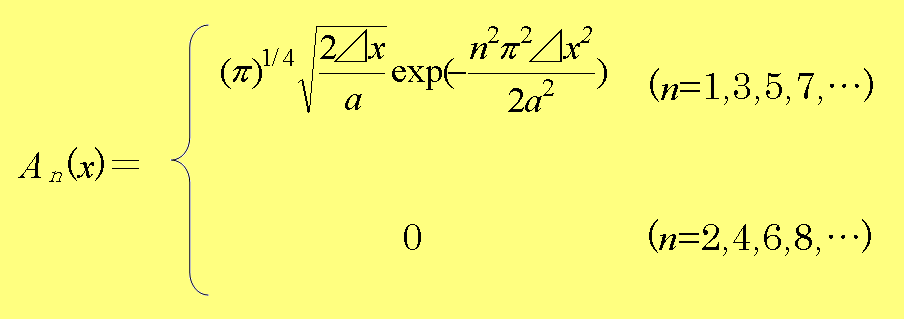 (1.97)
(1.97)
�ł���B�Ȃ��A���ꂼ��̏�Ԃ̃G�l���M�[���ʂ́A�悭�m���Ă���悤��
�@�@�@�@�@�@�@�@�@�@En=M/2�E{n��/(2a)}2 (M�F���q�̎���)�@�@�@�@�@ �@�@�@�@�@�@�@(1.98�j�@�@�@
�ł���B
�@��(x,0)����An��n�@�͖����a�ł��邪�V�~�����[�V�����͂����L���a�ŋߎ����čs�����߁AAn�̑傫�������ς���B
�@�@�@�@�@�@�@�@�@Am/A1��exp{-��2��x2(m2-1)/(2a2)}
���Am2-1��2a2/(����x)2�ł���AAm≈0�ƍl�����B�܂��Am�傫�ȏꍇ���Ă�m2-1≈m2�Ƃ��邱�Ƃ��ł���̂ŁA
�@�@�@�@�@�@�@�@�@m��1.414a/(����x)
�ł���Am+1�ȍ~��Am��0�Ƃ݂Ȃ����Ƃ��ł���B
�@a=0.5,��x=0.05�Ƃ���A
�@�@�@�@�@�@�@�@�@m��1.414�~10/3.14��4.5
�ł��邩��Am=5�ȍ~�̍���0�ƍl���Ă������x���Ȃ��B�������A���ۂ̃V�~�����[�V�����ɂ́Am=50�܂ł̍���p�����B(�����܂ŁA���߂Ă����Ζ����a�����߂��ꍇ�Ƒ卷�����ł��낤�B�j
�@���āA��������(1.63)�ɑ�����A���q�̊m�����x�̎��Ԃ�ω����v�Z���邽�߂ɂ́A�ʑ���n���߂Ȃ���Ȃ�Ȃ����A�܂������S��0�ł���Ƃ��ăV�~�����[�V�������Ă݂�Ɛ}1.8.1�`�}1.8.3�̂悤�ɂȂ�B�Ȃ��A���q�̎��ʂ�M=1�Ƃ����B
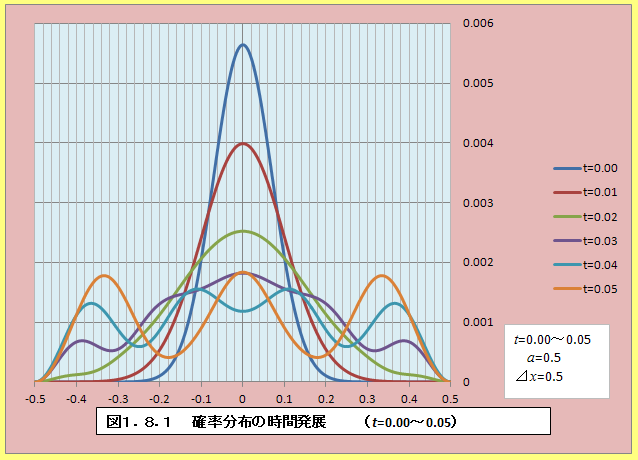
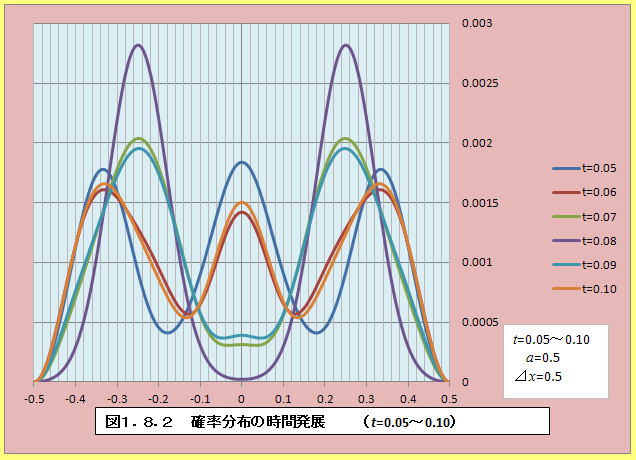
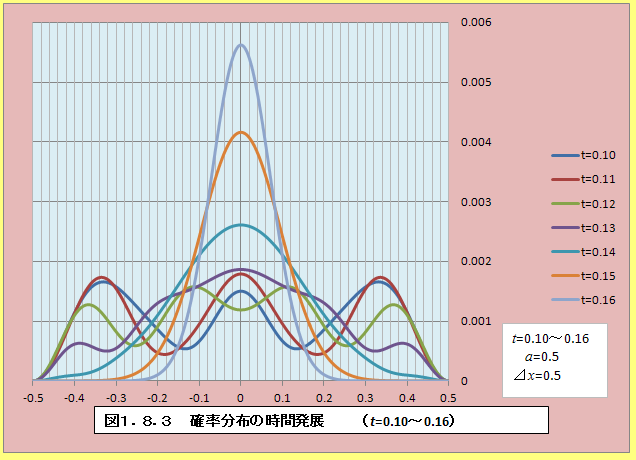
�@�T�ˁA����0.16�Ŋm�����z�̕ω����U�����Ă��邱�Ƃ��킩��B
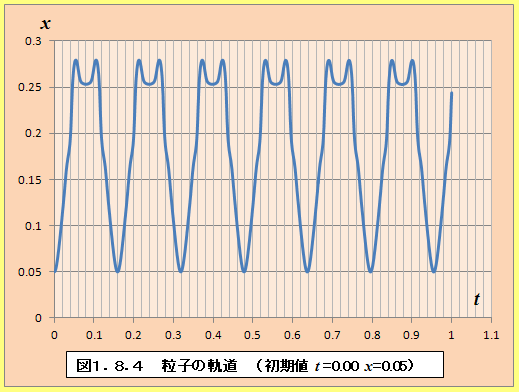
�@���̂��Ƃ́A��(1.69)�ɂ��^���ʂ����߁A���q�̋O�����O���t�ɂ��Ă݂�Ƃ�薾�ĂɂȂ�B�}1.8.4�́A�����l��x=0.05�Ƃ��āA���q�̋O�����v���b�g�������̂ł���B����ɂ��ƁA�T�ˎ�����0.154�ł���B���l�ɗl�X�ȏ����l�ɂ��āA���q�̋O�����v���b�g����Ɛ}1.8.5�̂悤�ɂȂ�B
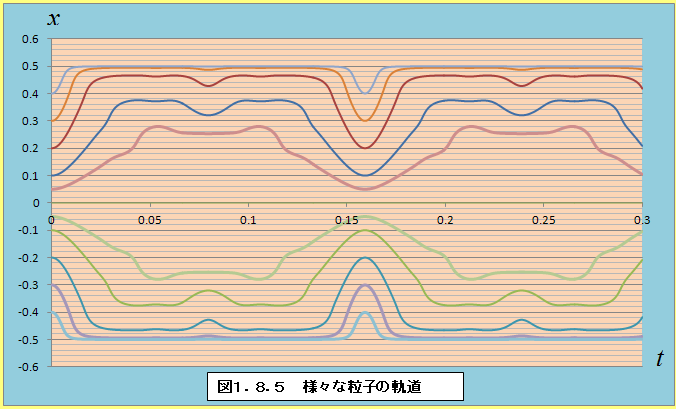
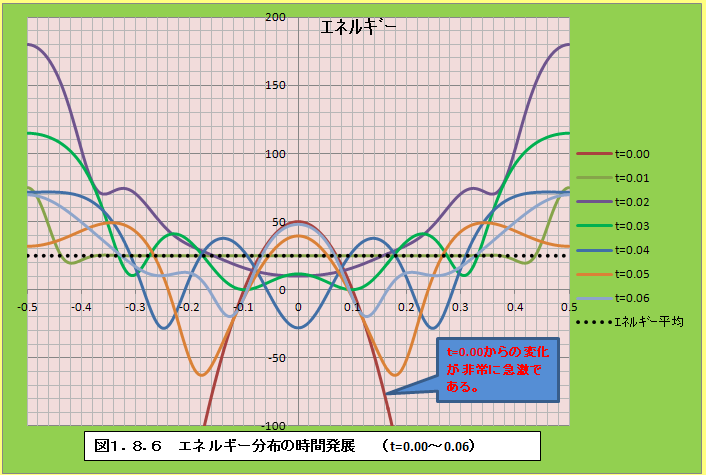
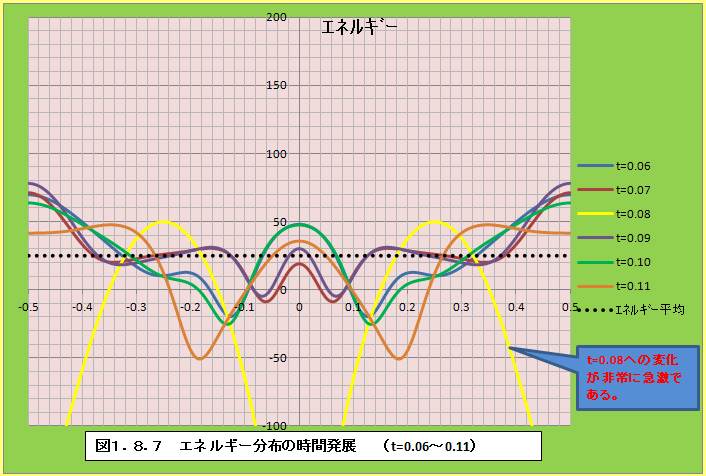
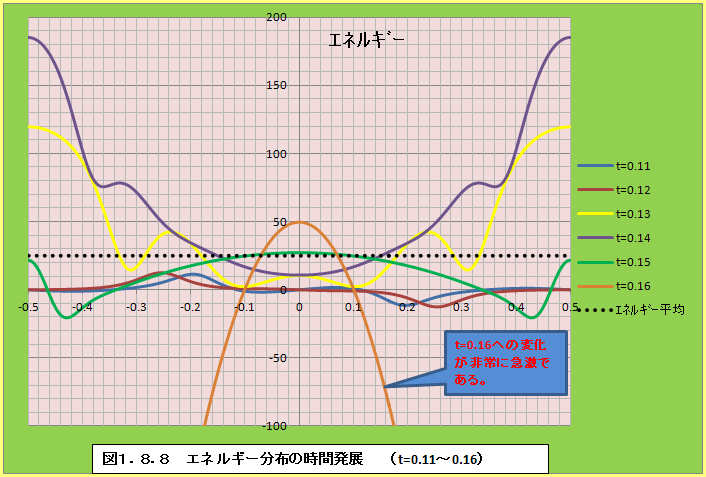
�@�����āA�}1.8.6�`�}1.8.8�͎�(1.87)�ɂ��A�G�l���M�[���z�����߂��̎��ԕω����v���b�g�������̂ł���B����ɂ��ƁAt=0.00,t=0.08,t=0.16�ŃG�l���M�[���z�̕ω������ɑ傫���Ȃ邱�Ƃ��킩��B�Ȃ��A�G�l���M�[���ς͎��ԂɈˑ�������Ɉ��ł��邪�A25.0�ł������B
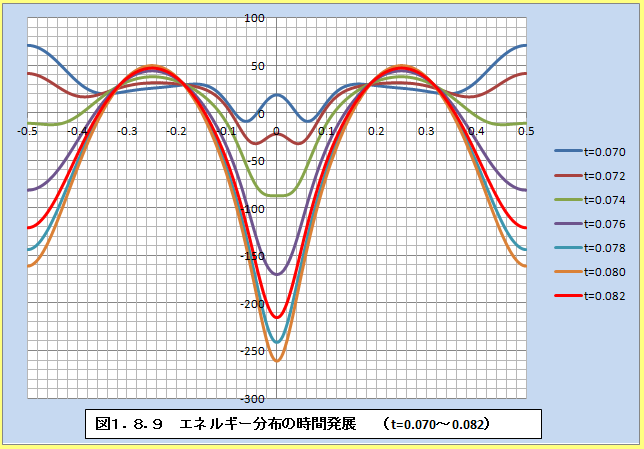
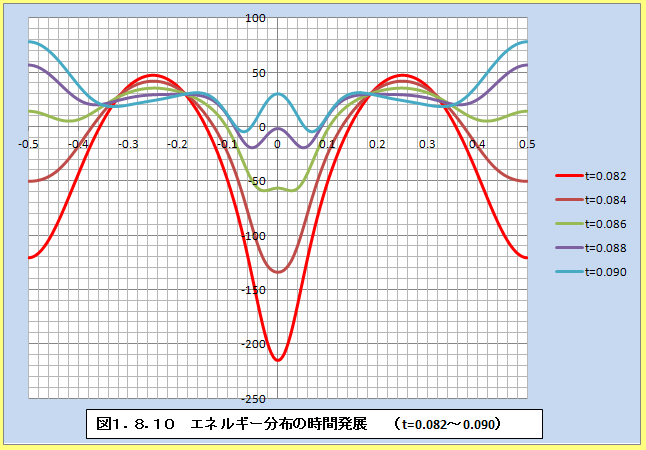
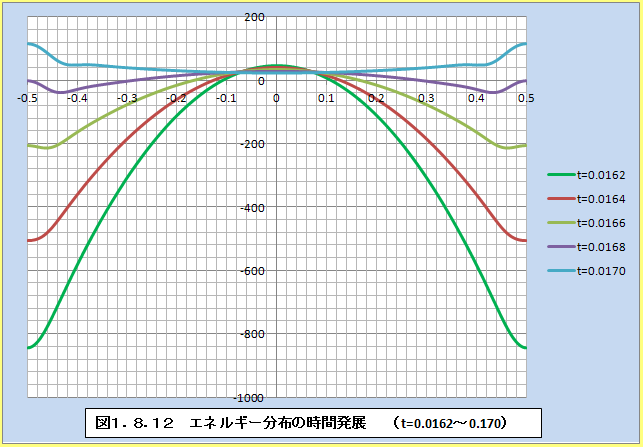
�@�ω����}���ȕ����ɂ��āA�����������Ԃ�Z�����ڍׂɃv���b�g����ƁA�}1.8.9�`�}1.8.12�̂悤�ɂȂ�B�Ȃ��A����������l����t=0.00��t=0.16�͓��l�ȕω��ɂȂ�Ǝv����B�����̃G�l���M�[�ω��́A���ԂƃG�l���M�[�ɂ��Ă̕s�m�萫�����ɂ����̂ł��邩��A�G�l���M�[���ς���̕ψʂ��傫���قǕω��������Ȃ�͓̂��R�ł���Bt=0.00,t=0.08,t=0.16�ŃG�l���M�[���z�̕ω������傫���Ȃ�̂́A���̂��Ƃ̕\��ƍl���邱�Ƃ��ł���B

�@���̃V�~�����[�V�����͎��߂ɑ����B
�����ؽ�т̗ʎq�͊w