ボーム力学

１．6　二重スリット２

１．6．１　度数分布のシミュレーション

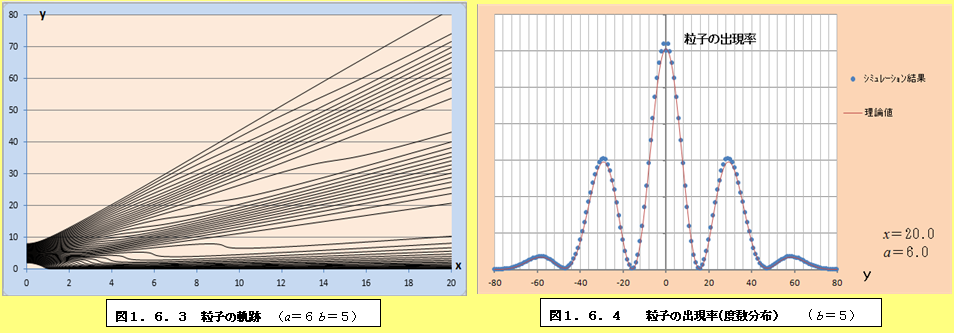
　本節では、より厳密に干渉の状況を見るために、粒子の度数分布を求めてみる。ここで注意しなければならないのは、初期状態での粒子の分布が一様では無いということである。例えば、ｘが正の側のスリットがx＝2からx＝8の範囲にあるとする。この場合の粒子の軌跡は、図1.6.3に相当するが、ここに描かれているのはt=0で粒子がスリットの中に一様に分布した場合の軌跡である。従って、図1.6.3の軌跡には粗密性が表れているが、それがそのまま度数分布になるのではない。

　では、初期状態(t=0)で粒子はどのような確率密度にあるかというと、前節の式(1.55)でt=0とすればよく

                 Ｐ(y,0)∝exp{-(y²+b²)/2(Δy)²}{exp(by／(Δy)²)＋exp(-by／(Δy)²)＋2} 　　　　　(1.6.1)

となる。このような、確率密度に従って初期状態を与え度数分布を求めればよいのであるが、実際に度数分布を求める際には次のような方法を用いてシミュレーションを行った。

　　　　　　　　�@ Δy＝1、スリットの幅をa=6、スリットの間隔を2bとする。(前節、図1.5.3参照)

　　　　　 �A y＝b−3からy＝b＋3の範囲で6/1000の間隔で10001個の点を取り、粒子のy座標の初期値とする。
　　　　　　　　（y座標が正の側の軌跡の初期値の設定）

　　　　　 �B 同様に、y＝-b−3からy＝-b＋3の範囲で6/1000の間隔で10001個の点を取り、粒子のy座標の初期値とする。
　　　　　　　　（y座標が負の側の軌跡の初期値の設定）

　　　　　　　　�C �A�Bで初期値を与えた粒子20002個について前節1.5.2のシミュレーションを行い、x=20(t=50)におけるそれぞれの
　　　　　　　　　　　　y座標を求める。(この結果を度数分布にしても、初期値を一様に与えただけなので正しい結果にはならない。）

　　　　　　　　�D �A�Bで設定した初期値をそれぞれ(1.6.1)に代入し、各初期値y_iに対して、初期状態の確率(p_i)を与える。

           �E �Cで求めた20002個のy座標について、n＝-100〜100と整数を取り、n-0.5≦y＜n+0.5の範囲にあるものをnにあると
　　　　　　　　し、それぞれの範囲にあるy_iについてp_iの和を求め、これをnにおける度数とする。
　　　　　　　　  (つまり、それぞれの初期状態の応じてp_i×１個として数える。なお、x=20(t=50)で20002個のほとんどがy＝-100〜100の範囲にある)

           �F �Eで求めた度数を全てのp_iの和で除算し、これを度数分布としてプロットする。(度数分布の規格化)

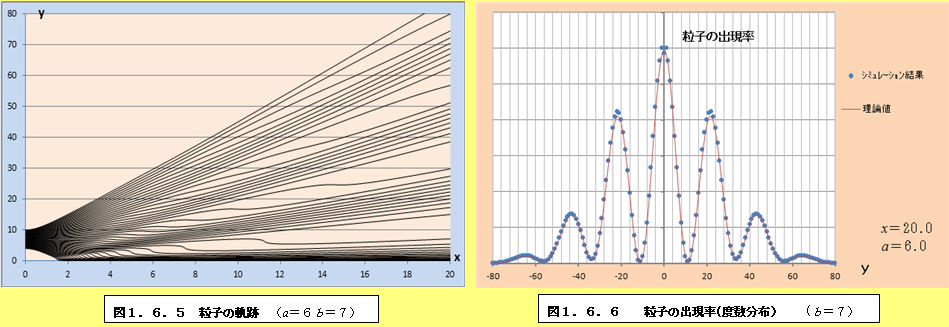
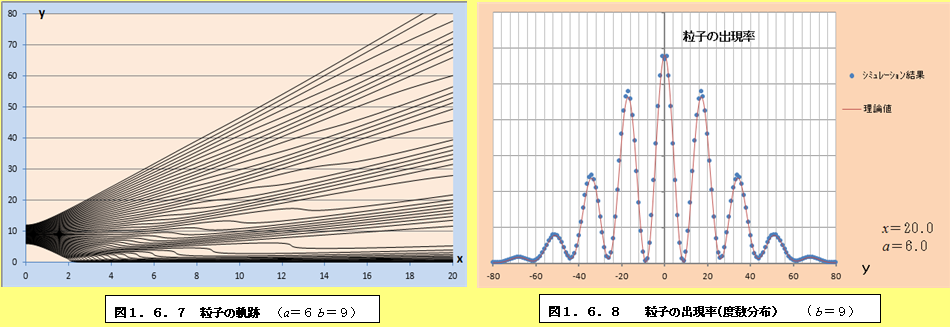
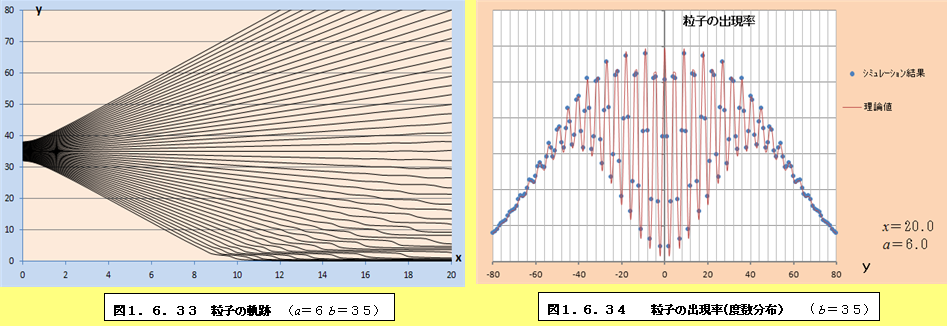
　このようにして、それぞれの場合について軌跡と粒子の出現率(度数分布)をプロットしたものが、図1.6.1〜図1.6.34である。理論値と比較すると、頂点付近で誤差が多少大きくなるものの、かなり大雑把な近似をしているにも関わらず、理論値に近い結果となっていることがわかる。また、スリットの間隔が大きくなるにつれて、徐々に干渉がぼやけて行く様子がわかるであろう。

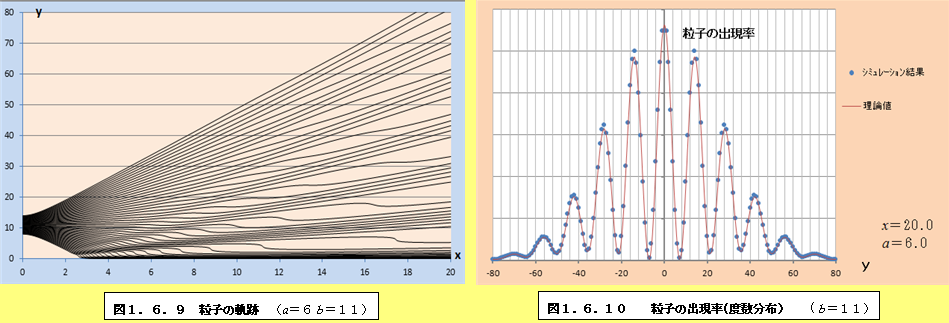
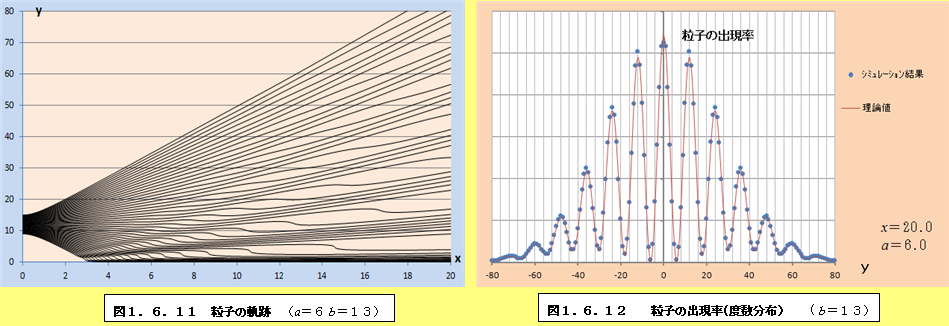
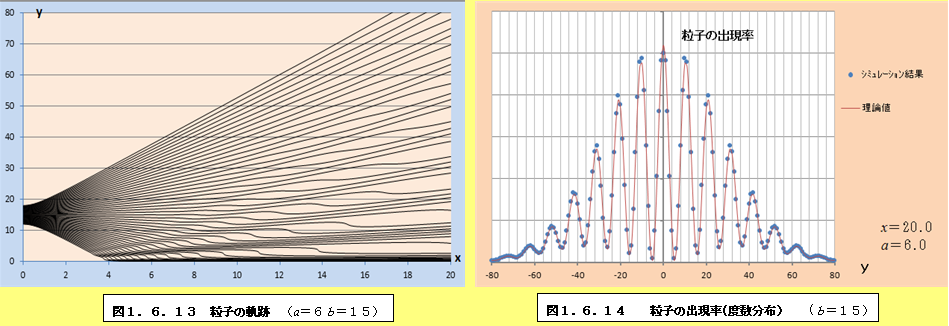
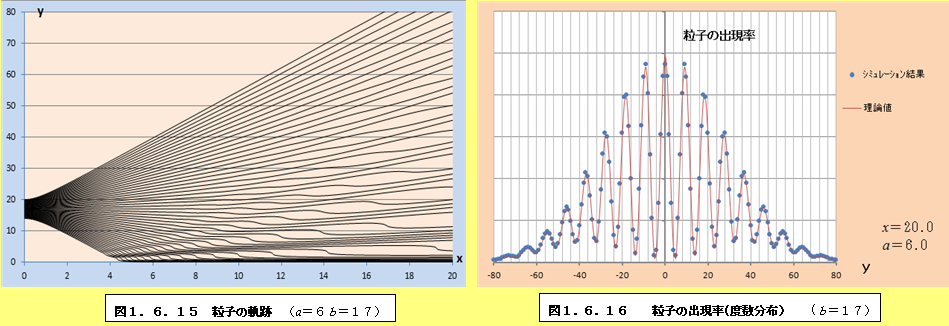
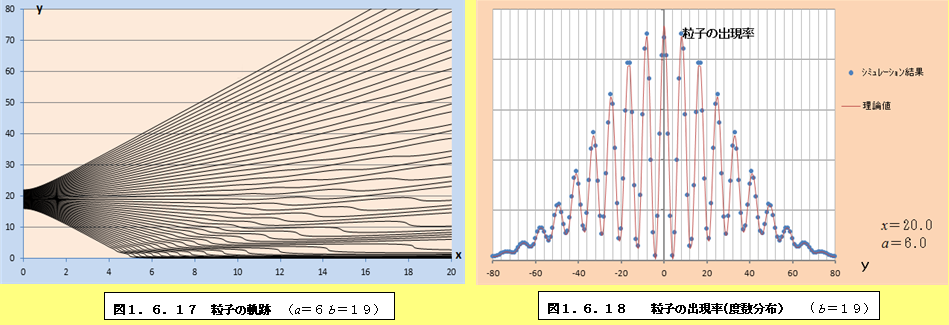
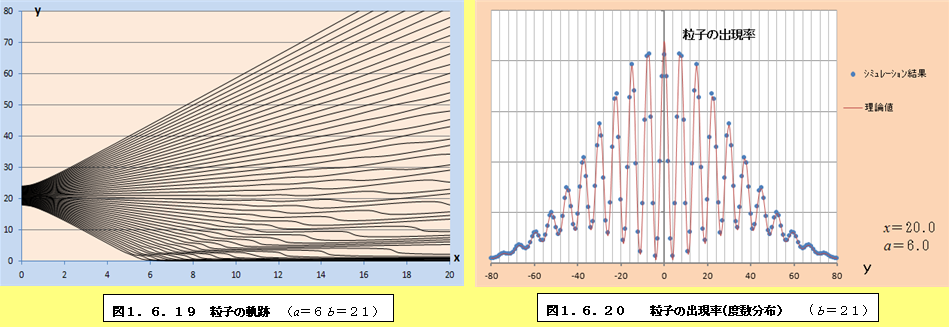
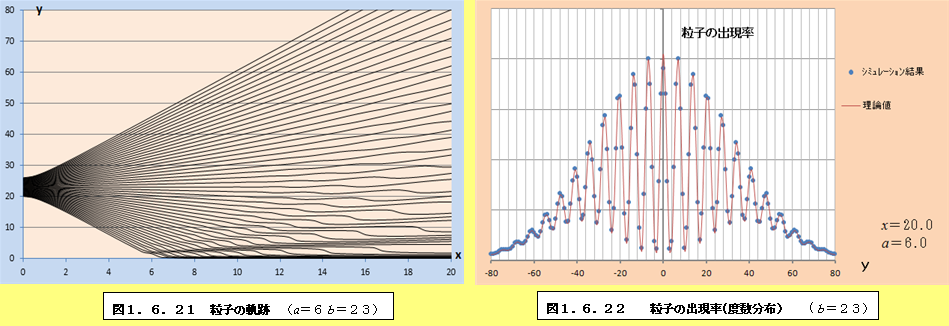
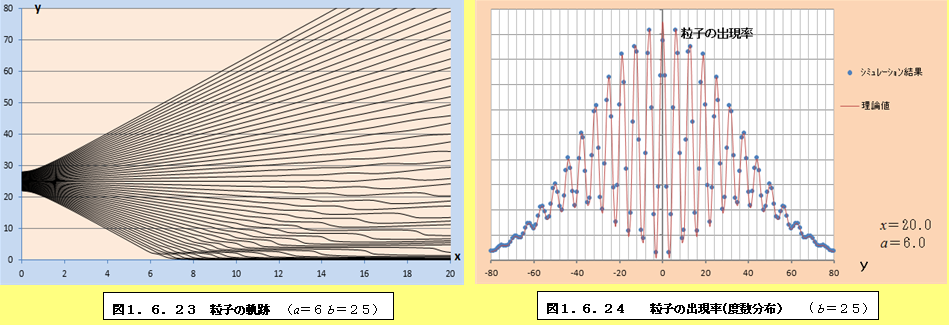
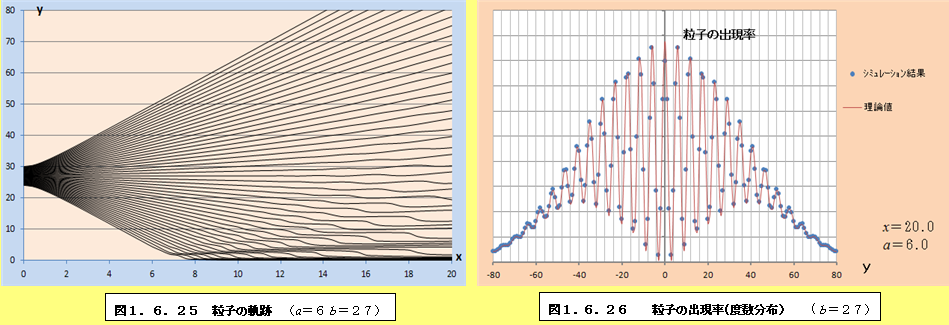
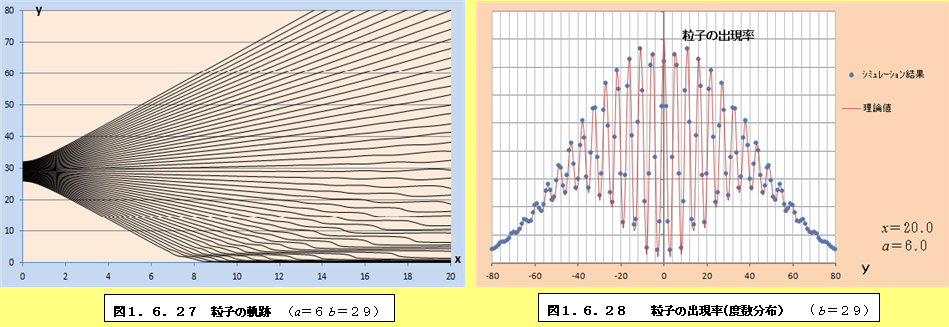
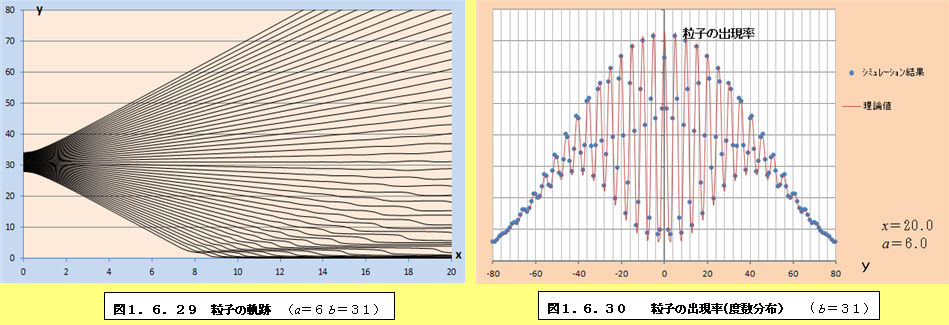
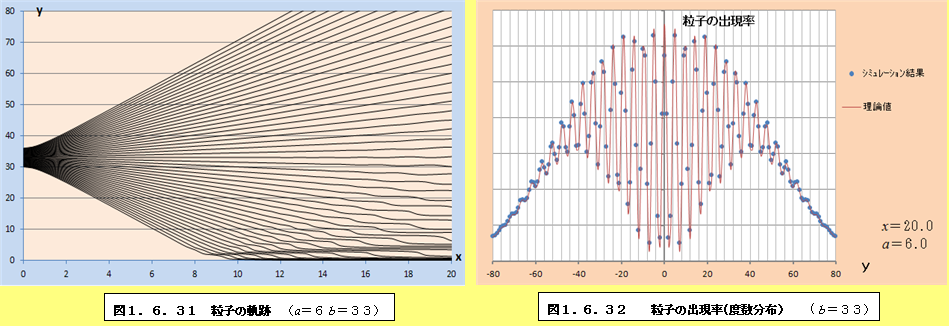
１．６．２　観測による干渉像消失の私的仮説

　図1.6.1〜図1.6.34の「粒子の出現率(度数分布)」のグラフを見ていくと、スリットの間隔bが大きくなるにつれて、粒子の出現率が極小値になるところと極大値になるところの間隔が徐々に狭くなり、干渉像がぼやけていくことがわかる。このことは、前節の式(1.55)

　　　　　　　　　　　　Ｐ(y,t)∝exp{-2(y²+b²)(Δy)²/σ_y}{exp(2Ａy)＋exp(-2Ａy)＋2cos(2Ｂy)} 　　　　　　　(1.55)

において、cosの項の振動が激しくなることにより生じ、極限では平均的にその効果が無くなり(平均的に0となる）、

　　　　　　　　Ｐ(y,t)∝exp{-2(y²+b²)(Δy)²/σ_y}{exp(2Ａy)＋exp(-2Ａy)} 　　　　　　　　　　　　　(1.56)

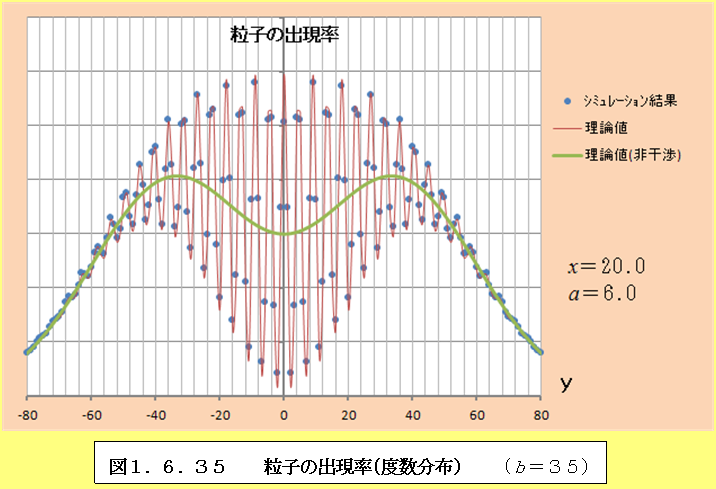
に近づくものと思われる。この(1.56)を「理論値(非干渉)」として表すと、b＝35の場合について図1.6.35のようになる。かなり揺らぎが大きいものの、粒子の出現率が式(1.56)に沿っていることがわかる。

　さて、二重スリットの実験には、「粒子がどちらのスリットを通り抜けるかを観測すると干渉像が消失する。」という奇妙な性質がある。このことは、観測による波束の収縮を仮定すれば次のように簡単に説明できる。(⇒が波束の収縮を表す）

　　　　　　　　(初期状態)　Ψ₁＋Ψ₂⇒      （終状態)　Ψ₁ or Ψ₂
　　　　　　　　　　　　　　Ψ₁ or Ψ₂のどちらに収束するかはわからないため、実験結果として得られる干渉像は、

　　　　　　　　 Ｐ(y,t)＝Ψ₁^*Ψ₁＋Ψ₂^*Ψ₂∝exp{-2(y²+b²)(Δy)²/σ_y}{exp(2Ａy)＋exp(-2Ａy)} 　　　　(1.57)

しかし、波束の収縮というのは、シュレディンガー方程式から出て来るものでもなく、これがあるとすればうまく説明ができるという単なる仮説である。そこで、式(1.57)と式(1.58)が一致することから、これも一つの仮説として、観測による干渉像の消失は式(1.55)のcos項の振動が激しくなるためではないか、ということもあり得るかと思う。つまり、実際には粒子がどちらのスリットを通るかを観測しても干渉は起きているが、それを観測することができないという立場である。そして、この場合cos項の振動が激しくなることの原因は、観測装置の作動による量子的な場の乱れということになる。

１．６．３　�I方向を一定速度としない場合の軌跡

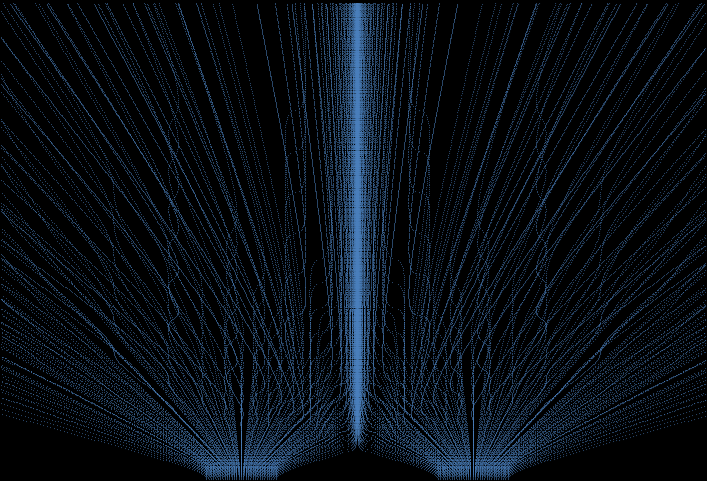
　これまで、ｘ方向の速さを一定としてシミュレーションを行って来たが、x方向にもガウス波束に従って運動するとした場合についての軌跡を最後の掲載し、本節の終わりとする。なお、��x＝1とした。軌跡が交差するため、全体的にぼやけていることがわかるであろう。

ボーム力学に戻る

ＴＯＰページに戻る

前に戻る　次に進む