�{�[���͊w
�P�D�R�@�����
�@�{�߂ł́A�������̒���Ԃ̃��f���ɑ��āA���ʓI���߂�K�p������B�܂��A���f���q�̂���Ԃ�����߂�ꂽ���R���q����ԓ��̂悤�ɁA�����g�����̒���Ԉ�ʂɂ��čl�@���Ă݂�B
�@����Ԃ̔g������(r,t)�͈�ʓI�ɁA
�@�@�@�@�@�@�@�@�@�@ ��(r,t)����0(r)exp(-iEt) (1.11)
�Ƃ����`�����Ă���B�����ł́A��0(r)�������̏ꍇ�ɂ��čl���Ă��邩��A��(1.1)�@��(r,t)��Rexp(iS)��K�p����ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@R����0(r)�@�@�@S��-Et�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@(1.12)
�ƂȂ�B���āA�܂�R����(1.6)�@�p ���|(1/2m)(��2R �^R) �ɑ�����ʎq�|�e���V���������߂邱�Ƃɂ��邪�A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�p ���|(1/2m)(��2R �^R)���|(1/2m)(��2��0�^��0)
�́A�V�����f�B���K�[����������A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�p ���|(1/2m)(��2��0�^��0)���o(H�|V)��0�p/��0��E�|V (1.13)
�ƂȂ�B�W�����_�ł́AE�|V�͉^���G�l���M�[�ƍl�����邪�A�{�[���͊w�ł͂��ꂪ�ʎq�|�e���V�����Ƃ����B���̂��Ƃ́A�ʎq�I�ȃn�~���g���|���R�r��������S�^�݂� �{(��S)2�^2m�{�u�{�p ��0��(1.12)�������Ă݂Ă��e�Ղɂ킩��B�܂��A(1.5)���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ p����S��0�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.14�j
�ƂȂ邱�Ƃ���A���q�͉^�����Ă��Ȃ����Ƃ��킩��B
�@�ȏ�́A���f���q�̂���Ԃ�����߂�ꂽ���R���q����ԓ��̂悤�Ȏ����g�����̒���Ԃł́A�ʎq�|�e���V�������ÓT�I�ȃ|�e���V�����̋�Ԉˑ���ł��������ߗ��q�ɗ͂���p�����i(1.13)���j�A�Î~���Ă���i(1.14)���)���Ƃ��������̂ł���A�W�����߂ƑS���قȂ錋�_�ł���B
�@���̂��Ƃ͐��f���q�̂���Ԃ��l����Ƃ���Ӗ��ō����I�Ȍ��_�ł���B�d���C�w�ɂ��ƁA�����^������d�q�͓d���g�͔����G�l���M�[���������߁A���q�j�̎��������^������d�q�̓G�l���M�[���������q�j�ɗ������ނ��ƂɂȂ�B����́A�ÓT�_�Ō��q���f�����\�������ۂɍŏ��ɂԂ���������ł��������A�d�q���Î~���Ă�̂ł���Γd���g����o���邱�Ƃ��������߁A����ԂɌ��肷��A���̍���͉�������邱�ƂɂȂ�B�Ȃ��AP��Ԃł�1.3.2�Ŏ����悤�ɁA�d�q�������^������Ƃ������_�������邽�߁A��͂�ÓT�I�Ȍ��q���f���͐��藧���Ȃ��Ȃ�B
�@�Ƃ���ŁA�ÓT�I�ȃ|�e���V������ł������A�ʎq�|�e���V�����͉�����Đ�����̂ł��낤���H����ɂ��āA�������邽�߂ɕK�v�Ȃ̂�information�̊T�O�ł���B���q���܂ތn�ɂ��Ă�information���A�ʎq�I�ȏ����ɂ���ĕ\����A���ꂪ�ʎq�|�e���V�����p ���|(1/2m)(��2R �^R)�Ƃ��������Ɉˑ����Ȃ���p�𗱎q�ɋy�ڂ��B�����āA���q�́A���̍�p�ɏ]�����^���̌`�����^�����A���̃P�[�X�ł́A���̉^���̌`�����A�ÓT�I�ȃ|�e���V�����̍�p��ł������悤�ɂȂ��Ă���̂ł���B
�@���āA����Ԃŗ��q���ϑ�����ƁA���ۂɐÎ~�������q���ϑ������悤�Ɏv���邪�A�����ł͂Ȃ��B����ɂ��ẮA�{�[���̊ϑ����_�Ŏ������̂ł��邪�A�ϑ��̏�ɂ��ʎq�I�ȏꂪ�ω����A���q����������邽�ߐÎ~�������q���ϑ��ł���킯�ł͂Ȃ��B���̂��Ƃɂ��ẮA������ڍׂɏq�ׂ邱�ƂƂ���B�Ȃ��A�ϑ�����闱�q�̈ʒu�́A�A���T���u��������R2�ɂȂ�(1.1.3�̇D)���Ƃ��A���ʓI���߂ł��W�����߂Ɠ����m�����z�ɉ����Ċϑ�����邱�ƂɂȂ�B
�@
�P�D�R�D�Q�@���f���q�̂Q�o���
�@�{�[���͊w�ł́A�g�����̋�Ԉˑ��������ł������Ԃ́A���q���Î~���Ă���Ƃ������Ƃ��O�߂Ŏ����ꂽ���A���ɔg�����̋�Ԉˑ��ɋ������܂ޗ�Ƃ��āA���f���q���f���̂Q�o��Ԃɂ��čl���邱�ƂƂ���B
�@�Q�o��Ԃ̔g�����́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��(r,��,��,t)��f(r,��)exp(im��)exp(-iEt) (m��-1,0,1:���C�ʎq��) (1.15)
�Ƃ����`���ł���Bf(r,��)�́A���ׂĎ����ł��邱�Ƃ��玮(1.1)�@��(r,t)��Rexp(iS)��K�p����ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@R��f(r,��)�@�@�@S��-Et +m�� (1.16)
�ł���B�Ȃ��A�Q�o��Ԃ͎�ʎq����2�ł��邱�Ƃ���AE���|1�^8�ƂȂ�B(���q�P�ʌn��p���Ă��邱�Ƃ���A�d�q�f�ʁ��d�q���ʁ��{�[�A���a��ћ��1�ł���)
�@�܂��AR����(1.6)�@�p ���|(1/2m)(��2R �^R) �ɑ�����ʎq�|�e���V���������߂邱�Ƃɂ���B�ʓ|�Ȍv�Z������邽�߃V�����f�B���K�[�������𗘗p���邪�A���̂��߂̏����Ƃ��ĉ��Z�q��2��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@��2����2/��r2�{2/r�E��/��r�|1/r2sin���E��/�����E(sin�Ɓ�/����)�|1/r2sin2���E��2/����2
�@�@�@�@�@�@�@�@�@�@�@�@ ���`(��/��r,��/����)�|1/r2sin2���E��2/����2 (�`(��/��r,��/����)�́A��/��r����/�����ō\������鉉�Z�q)
�Ƃ����B��������ƁA���f���q���f���̃n�~���g�j�A���́A
�@�@�@�@�@�@�@�@�@�@�g���|(1/2)��2�|1/r���|(1/2)�`�|(1/2)�E1/r2sin2���E��2/����2 �|1/r�@�@�@�@�@�@�@ (1.17)
�ƂȂ�A����Ԃ̃V�����f�B���K�[�������́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�|(1/2)�`�|(1/2)�E1/r2sin2���E��2/����2 �|1/r)��(r,��,��)��E�� (r,��,��) �@�@�@�@�@�@�i1.18�j
�ł���B����ɁA��(r,��,��)��f(r,��)exp(im��)��R(r,��)exp(im��)��������ƁAm=�}1�ł�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�|(1/2)�`R�{(1/2)�ER/r2sin2���|R/r)exp(im��)��ERexp(im��) �@�@�@�@�@�@�@�@�@�@�i1.19�j
�ƂȂ邪�A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�|(1/2)��2R���|(1/2)�`R�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.20�j
�ł��邽�߁A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�p ���|(1/2)(��2R
�^R) ���|(1/2)(�`R)�^R
�@�@�@�@�@�@�@�@�@�@�@�@�@���|(1/2)�E1/r2sin2���{1/r�{E�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.21�j
����āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�p�{(1/2)�E1/r2sin2���|1/r��E�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i1.22�j
�ƂȂ�B
�@���āA(1.22)�̍��ӂ����Ă݂�ƁA��R���͌ÓT�I�ȃ|�e���V����(V���|1/r)�ł��邱�Ƃ����炩�ł���B����A��Q���� p����S��(1.16)�������Čv�Z���Ă݂�ƁA
�@�@�@�@�@�@�@�@�@�@p����S ����(-Et +m�� )��me�� /r sin���@�@�@�@(e���́A���̓��a�����̒P�ʃx�N�g��)�@�@�@�i1.23�j
�ƂȂ�A�����ʎq�I�ȃn�~���g���|���R�r��������S�^�݂� �{(��S)2�^2m�{�u�{�p ��0�ɑ������ƁA(1.22)�Ɠ������ʂ�������B����̌��ʂ�������͓̂��R�̂��Ƃł��邪�A�ʎq�I�ȃn�~���g���|���R�r�������̍��ӑ�Q�����A(1.22)�̍��ӑ�Q���ɑΉ����Ă���A(1.22)�̑�Q���͉^���G�l���M�[��\�����̂ƍl���邱�Ƃ��ł���B
�@�]���āA���f���q���Q�o���(m=�}1 )�ł͓d�q�͐Î~���Ă���̂ł͂Ȃ��A�^�����s���Ă��邱�Ƃ��킩��B�Ȃ��Am��0�̏ꍇ�́A�g�����̋�Ԉˑ������������ł��邽�ߗ��q�́A�Î~�����܂܂ł���B
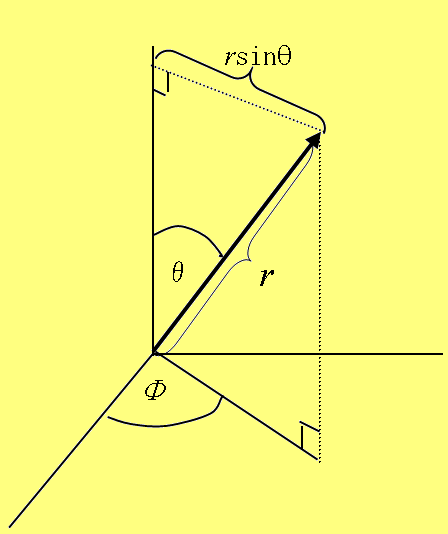
�@���āA(1.22)�̍��ӑ�Q����A(1.23)�̍Ō�ɂ���r sin�Ƃ́A���̉�]������̋����ƂȂ�B�ȒP�ɐ}������A�}1.3.1�̂悤�ȊW�ɂȂ�B�Ȃ��A�������̉�]���͒ʏ킚���Ƃ��Ē�`�����B

�@�����ŁA����r sin���Ƃ����A(1.21)��
�@�@�@�@�@�@�@�@�@�@�@�@ �p ���|(1/2)�E1/��2�{1/r�{E �@�@�@�@�i1.24�j
�ƂȂ�B�]���āA�ÓT�I�ȃ|�e���V����V���|1/r�Ɨʎq�|�e���V�����p�̘a�́A
�@�@�@�@�@�@�@�@�@�@�@�@�p�{V���|(1/2)�E1/��2�{E
�ł���B������A��(1.9) mdv�^dt���|��(�u�{�p)�ɑ������ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ dv�^dt���|1/��3e���@�@�@(m=1�Ae�������̑�����������̒P�ʃx�N�g��)�@�@ �@(1.25)
�ƂȂ�B�܂�A�|�e���V�����ɂ���ė��q�ɍ�p����͂̕����́A��������Ɛ������������ł���B
�@���āA���̓������̗͂Ƌt�����ɍ�p���鉓�S�͂��ŏ��������A���q�������𒆐S�Ƃ���~�^�����s�����ƂƂȂ邪�A�~�^���̉��S�͂́A
�@�@�@�@�@�@�@�@�@�@�@�@mv2/����p2/����1/��r2sin2����1/��3
�ł���A(1.25)�Ƒŏ����������Ƃ��킩��B�]���āA�Q�o���(m=�}1 )�̗��q�͂��������Ƃ�����]�^�����s���Ă��邱�Ƃ��킩��B
�����ؽ�т̗ʎq�͊w