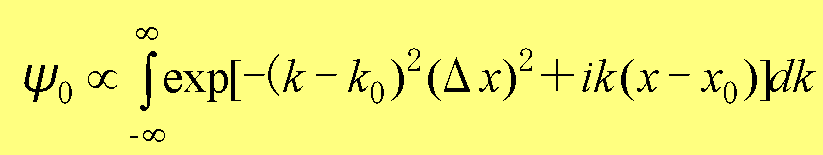(1.26)ボーム力学
１．4 ガウス波束
１．４．１ ガウス波束
本節では、非定常状態の例として、ガウス波束について扱うこととする。
まず、位置x＝x0を中心とし、運動量(＝波数：原子単位系ではћ＝１）の平均がk0であり、位置の不確定性がΔxである一元のガウス波束の波動関数は、
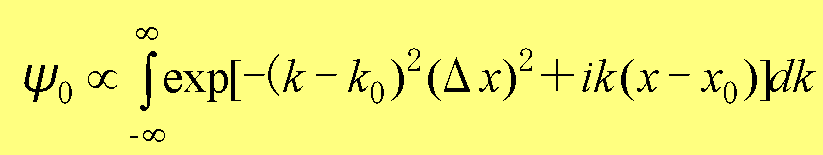(1.26)
となる。なお、量子ポテンシャルや運動量を求める際には、規格化定数は特に問題ならないため、比例関係(∝)だけを用いて記載している。式(1.26)の形から明らかなように、これは自由粒子の運動量kの固有状態ψk＝exp(ikx)をすべて重ね合わせた波動関数である。定常状態の重ね合わせであることを、強調的して記載するなら、ｃk＝exp[-(k-k0)2(Δx)2-ikx0]とし、kの積分をΣで置き換えれば、
ψ0 ∝ Σｃkψk
となる。さて、自由粒子の質量m=1とすれば、運動量kの固有状態ψkのエネルギーはEk＝k2/2である。（定常状態のシュレディンガー方程式に代入）従って、時間に依存する重ね合わせの状態は、
ψ（x,t） ∝ Σｃkψkexp(-iEkt)＝Σｃkψkexp(-ik2t/2)
となり、これが定常状態の重ね合わせであり、非定常状態となっていることがわかる。再び、Σを積分に置き換えると、
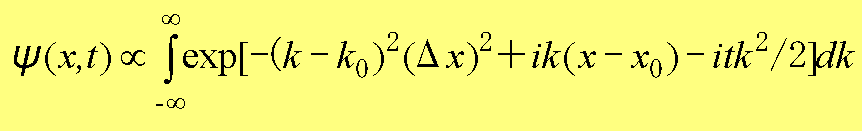(1.27)
となる。式(1.27)の積分を行うには、
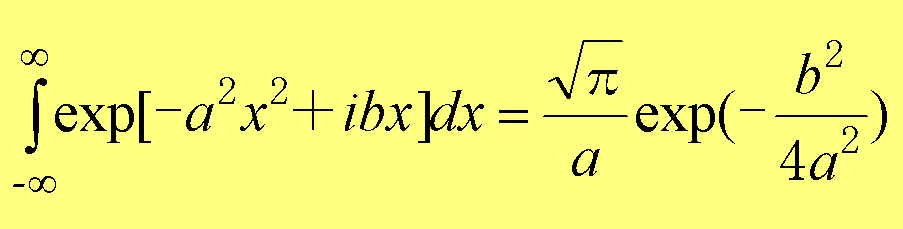(1.28)
という公式を用いる。すると、
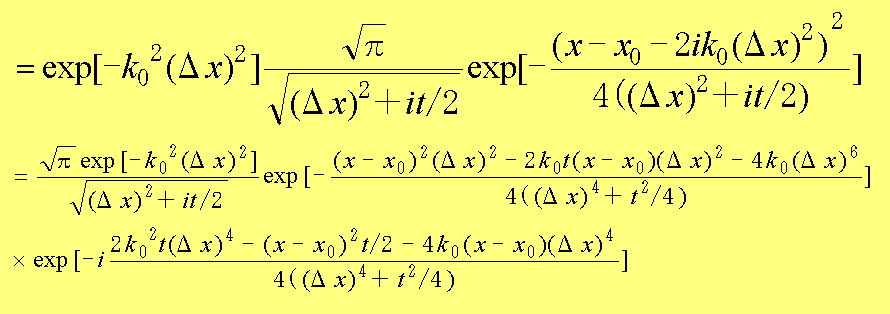(1.29)
のようになる。
さて、式(1.29)は３つの因子の積からなっているが、第１因子は、式(1.5)により運動量を求める場合も、式(1.6)により量子ポテンシャルを求める場合にも、無視して差し支えない項である。その理由は、
(Δx)2+it/2=rexp(iθ) （rとθはいずれも、実数とする）
とおけば、tanθ＝t/2(Δx)2 、r＝((Δx)4+t2/4)1/2となり、式(1.1) Ψ(r,t)＝Rexp(iS)に当てはめれば、
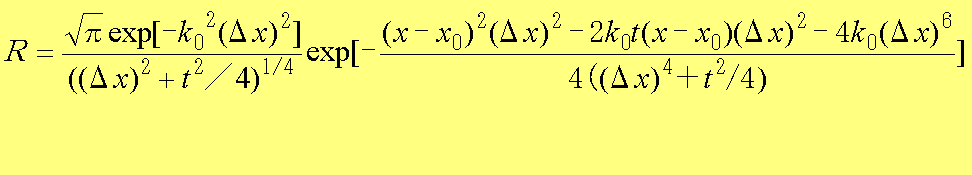(1.30)
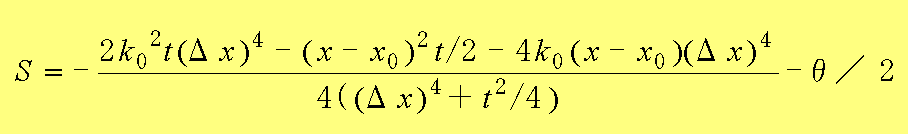(1.31)
となり、xに依存しない式(1.29)の第一因子は、運動量と量子ポテンシャルの計算結果に関係しないからである。
まず、計算が簡単な運動量を、式(1.5) p＝∇S により求めると、
p＝｛(x−x0)t＋4k0((Δx)4｝／(4(Δx)4＋t2)・ex (exはx方向の単位ベクトル) (1.32)
となる。
続いて、量子ポテンシャルを、式(1.6) Ｑ ＝−(1/2m)(∇2R ／R) により求めると、
Ｑ ＝(Δx)2／(4(Δx)4＋t2)−2(Δx)4(x−x0−k0t)2／(4(Δx)4＋t2)2 (1.33)
となる。なお、 m＝1としているため式(1.33)にmは表れず、式(1.32)のpは速度と等しいことに注意。
さて、式(1.32)は、時刻t＝0にx0を中心とするΔxの中、つまりx0−Δx/2≦x1≦x0＋Δx/2という領域内に粒子があった場合に、その後ガウス波束の影響を受ける粒子の運動を表している。k0は、ガウス波束自体の速度となる。例えば、x0＝0、k0＝0.2、Δx=1とした場合に、t＝0でxの初期値を与えて運動の様子をシミュレーションすると図1.4.1のようになる。
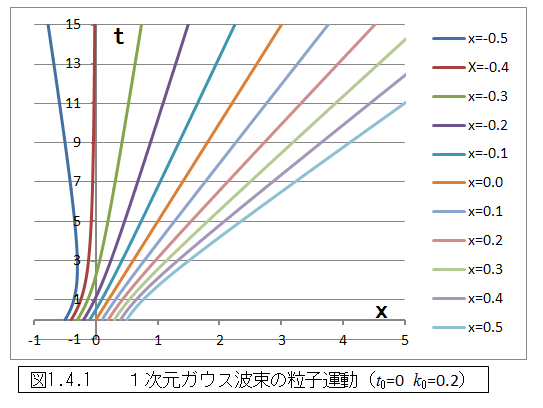
図1.41を見るといずれの軌道もある程度時間が経過すると、一定の速度の収束することがわかる。このことは、式(1.32)を解けば容易に理解できる。
質量を1としているため、運動量は速度に等しい。そこで、式(1.32）は、
dx/dt＝｛(x−x0)t＋4k0((Δx)4｝／(4(Δx)4＋t2) (1.34)
という微分方程式になる。式(1.34)は、このままでは変数分離形にはならないが、特殊解としてx＝k0t＋x0が容易に求まる。これは、図1.4.1で初期値がx＝0.0の場合に相当する。ここで、x＝k0t＋x0＋f(x)とおくとf(x)が容易に求まり、
x＝c1(t2＋4(Δx)4)1/2＋k0t＋x0 (c1は定数) (1.35)
となる。ここで、再度式(1.35)をtで微分すると、
dx/dt＝c1t／(t2＋4(Δx)4)1/2＋k0 (1.36)
となる。式(1.36)は4(Δx)4<<t2では、
dx/dt ≈c1＋k0
であり、t が大きくなれば、速度は一定となることがわかる。
さて、tでの粒子の位置x1を初期条件として与えると、式(1.35)は定数c1が求まり、
x＝(x1−x0)/2(Δx)2・(t2＋4(Δx)4)1/2＋k0t＋x0 (1.37)
となり、速度は、
dx/dt＝(x1−x0)/2(Δx)2・t／(t2＋4(Δx)4)1/2＋k0 (1.38)
であり、4(Δx)4<<t2では、
v＝dx/dt ≈(x1−x0)/2(Δx)2＋k0 (1.39)
となる。ここで、x1＝x0＋Δx/2の場合とx1＝x0−Δx/2の場合のvの差Δvを求めると、
Δv≈1/2Δx ∴ΔvΔx≈1/2 さらに質量1のため、ΔpΔx≈1/2
となるが、これは不確定性原理を表している。ガウス波束は、そもそもΔpΔx＝1/2が成り立つものとして定義されているが、ボーム力学を介しても、同様な結果が得られる。ここで、注意しなければならないのは、ここでいう初期値は概念上利用できるが、実際に観測して知ることができないということである。我々は、一定の範囲Δxのどこかに粒子が実在ということは言えても、それがΔxのどこであるを実際に知ることができず、それゆえに式(1.37)によっても、その後の粒子の位置を特定することはできない。ボーム力学は、古典力学と同じように、因果的であるが決定論的では無いというのは、このような意味である。
１．４．２ ガウス波束の収縮
ガウス波束の量子ポテンシャルは(1.33)で与えられるが、一見すると非常に複雑な形をしているが、これを実際にグラフで表してみると、図1.4.2及び図1.4.3のような単純な形をしている。
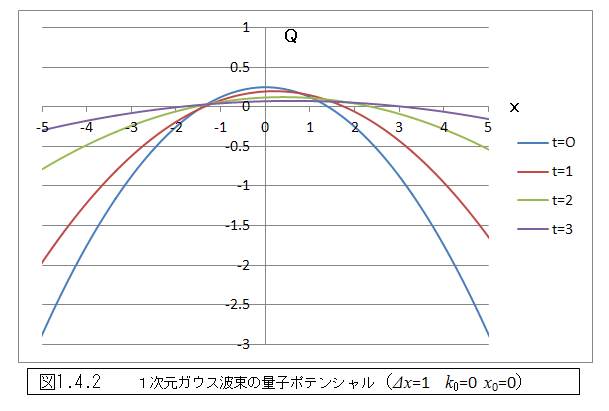
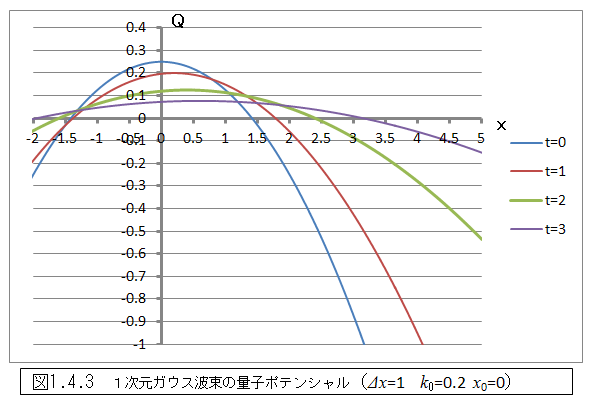
図1.4.2は、k0=0の場合であるが量子ポテンシャルの極大値が、時間とともに小さくなっていき徐々に平坦になっていることがわかる。これは、最終的にポテンシャルが一定となり、速度が一定の値に収束するという、式(1.36)の結論と整合するものである。なお、t=0でxの絶対値が大きいと量子ポテンシャルの勾配も非常に大きいが、粒子は−Δx/2≦x1≦Δx/2の範囲にあるため、その影響を受けることはない。
さて、量子ポテンシャルを表す、式(1.33)は、
Ｑ ＝(Δx)2／(4(Δx)4＋t2)−2(Δx)4(x−x0−k0t)2／(4(Δx)4＋t2)2 (1.33)
であるが、これは位置と時間の関数になっているが、粒子の軌道を与えればその粒子が任意の時間にある位置の量子ポテンシャルを与えることができる。つまり、式(1.37)のxを代入すれば、t=0でx=x1にあった粒子が、任意の時間にある位置の量子ポテンシャルを求めることができ、
Ｑ(t) ＝((Δx)2−x12／2)／(4(Δx)4＋t2) (1.40)
となる。同様にして、運動量(＝速度：質量=1のため)も求まり、
Ｐ(t) ＝(x1−x0)/2(Δx)2・t／(t2＋4(Δx)4)1/2＋k0 (1.41)
となり、これは式(1.38)と同じである。この結果を、量子的なハミルトン−ヤコビ方程式∂S／∂ｔ ＋(∇S)2／2m＋Ｖ＋Ｑ ＝0に代入すれば、任意の時刻におけるエネルギーを求めることができ、
E＝−∂S／∂ｔ＝(∇S)2／2m＋Ｖ＋Ｑ ＝Ｐ(t)2／2＋Ｑ(t)
＝1/2・{(x1−x0)2/4(Δx)4・t2／(t2＋4(Δx)4)＋k02＋(x1−x0)/(Δx)2・k0t／(t2＋4(Δx)4)1/2}＋((Δx)2−x12／2)／(4(Δx)4＋t2)
(1.42)
となる。ここで、t →∞とすると、
E →1/2・{(x1−x0)2/4(Δx)4＋k02＋(x1−x0)/(Δx)2・k0}＝1/2・{(x1−x0)/2(Δx)2＋k0}2 (1.43)
となる。このことは、速度が式(1.39)に従い一定となり、t →∞で量子ポテンシャル→0になることからも当然の帰結である。しかし、連続的な変化でエネルギーが一定の状態になるというのは、非定常状態が連続的変化で定常状態に変化することを意味しており、標準解釈で波束の収縮に該当するものである。なお、ここでは敢えてエネルギーを用いたが、運動量固有状態についても同様なことが言え、式(1.39)がこれを表している。
標準解釈との違いをもう少し詳しく説明すると、ガウス波束式(1.27)をΣを用いて記述すると、
ψ（x,t） ∝ Σｃkψkexp(-iEkt)＝Σｃkψkexp(-ik2t/2) (1.44)
であり、標準解釈ではこれをψk状態の重ね合わせの状態とし、運動量の観測によりある１つの状態ψsに収束すると考える。この時の収束過程は、射影演算子により行われる非因果的で非連続的な変化とされ、観測をする直前までの状態は(1.44)のままであるとする。
これに対して、ボーム力学は、どこにあるかはわからないにしても、図1.4.1のような軌道のどれかに粒子が実在しているものと考える。そして、ある程度の時間(原子単位系では、t=1は光がボーア半径を移動する時間(a0/c)である）が経過すれば、式(1.39)により運動量は一定の値にほとんど収束しており、観測する直前においても状態はψsであると考えることができ、非因果的で非連続な変化を避けることができる。さて、そうするとボーム力学では標準解釈でいう干渉のような現象が起こらないのかというと、そうではない。図1.4.1で言えば、軌道が直線となっていない領域では、他の運動量固有状態との干渉が起きていると考えることができる。そして、各軌道が位置的に徐々に分離していくにつれて、干渉による効果が徐々に小さくなっていくと考えることができる。
ところで、最初に波動関数が実数の定常状態に粒子があり、ある位置にΔxの精度で粒子を観測したとする。この位置をx=0とし、最初にあった波動関数を無視すれば、粒子の後、k0=0，x0=0のガウス波束(φ0)に従って運動するものと考えられる。そして、比較的長い時間Tが経過した後に、再び粒子をある位置x=x1で観測すれば、今度は粒子がk0=x1/T，x0=x1のガウス波束(φ1)によって運動するものと考えられる。この時k0=0，x0=0ガウス波束からk0=x1/T，x0=x1のガウス波束が分離したと考えると、再び「information」という概念が浮かび上がる。つまり、φ0=φ1＋φ2＋φ3＋φ4＋・・・・というように互いに干渉しない程度にガウス波束が分離され、粒子の運動に影響するのは粒子を含んでいるガウス波束φ1のみであり、このφ1が「active-information」に該当し、φ2 ，φ3 , φ4,・・・・が「passive-information」に該当する。この例では、一度「passive-information」となったガウス波束が粒子の運動に、その後影響を与えることは無いであろうが、もし一度分離したガウス波束をφ1と干渉させるができれば、潜在的に存在していた「passive-information」を再び「active-information」にすることができる。このような例の一つが、二重スリットによる粒子の干渉現象である。次節では、実際にボーム力学による二重スリットのシミュレーションを行ってみたい。
s
ｱﾏﾁｭｱﾘｽﾞﾑの量子力学