ボーム力学

１．１　ボーム力学の出発点（量子ポテンシャル）

　「量子力学は、実験結果の確率を計算するアルゴリズムを含んでいるが、個々の量子プロセスの物理的内容を与えるものではない。実際のところ、結果が示される測定装置が無ければ、量子論の方程式は全く物理的な意味を持たない単なる数学であろう。また、それゆえに量子論は、測定装置がどのように機能するかの(一般的にいって統計的な)知識を与えるだけにすぎない。・・・BohrやHeisenbergが示したように、量子論は、少なくとも可能な限りにおいて、実在についての我々の認知と、この実在の振る舞いを予測し操作する方法についての我々の知識にのみ関係するだけである。あるいは、もっと哲学的な術語を用いるなら、量子力学は認識論的であると言えるだろう。なお、認識論とは、我々が知識をどのようにして得るかという問いに着目した考え方をいう。
　このことから、量子力学は実在それ自身について、ほとんど何も言うことができないといえる。哲学的な術語を用いれば、量子力学は、量子系に対して存在論と呼ばれるものを何も与えないということである。存在論とは、第一義的にどうあるかに着目し、そこから知りうることについては副次的な意味を持つに過ぎないような考え方をいう。（例えば、観測される系と観測装置があることを知っているか、知らないかに関係なく、それらがともに存在するものとみなされ、観測される系と観測装置の間の相互作用として観測の過程を扱うことが、存在論的な考え方である）・・・・」

　非常に拙い訳で、理解しにくいであろうが、『THE UNDIVIDED UNIVERSE』のChpter１からの引用である。

　粒子の位置と運動量を同時確定的知ることができないのなら、同時確定的な位置と運動量はそもそも存在しない、つまり「観測できないものは存在しない」と考えるのが量子力学の標準解釈である。このような立場は、「我々が知り得るものだけを対象とする」という意味で認識論的である。しかし、そうすると量子力学は実験結果のような「知り得るもの」の確率を計算するアルゴリズムを示すもので、観測の有無に関わりなく存在するような実在については、何も表していないということになり、このことが上述では批判的に述べられている。ここでは深く立ち入らないが、このような批判はChpter2でさらに詳細に論証される。

　そして、認識論的に量子論を解釈していることが、次のような問題が引き起こしているという。

�@量子論は、統計的なアンサンブルを扱うのには問題ないが、波束の収縮のような問題のある前提を用いないと
　　個々の量子過程を表すことができないこと。

�AEPR等でよく知られている非局所性の問題があること。

�B量子干渉実験で証明された、ものの性質であるミステリアスな「波と粒子の二重性」があること。

�C何よりも、量子的な系の実在が何であるかという、明確な概念を与えることができないこと。

　現在ではあまり問題とされていないが、直観的に理解できないという意味ではこれらは解決されたとも言えない。存在論的解釈は、上記のような問題をある程度直観的に理解しやすい形で表し、標準解釈(認識論的解釈）と同じ結果を導くことが可能である。

１．１．２　量子ポテンシャル

　ボーム力学の出発点となるのが、量子ポテンシャルであり、次のようにしてシュレディンガー方程式から導かれる。

　まず、波動関数Ψ(r,t)を、

　　　　　　　　　　Ψ(r,t)＝Rexp(iS)   　　（RとSは実数であり、いずれもrとt の関数とする）　　　　（1.1） 

とおき、これをシュレディンガー方程式 i∂Ψ／∂ｔ　＝(−∇²／2m＋Ｖ )Ψ に代入すると、簡単な計算により、

　　　　　　　　　　　　　　∂S／∂ｔ ＋(∇S)²／2m＋Ｖ−(1/2m)(∇²R ／R)＝0                          (1.2)

                   ∂R²／∂ｔ ＋∇・(R²∇S／m)＝0　　　　　　　　　　　　　　　　　　　　　   (1.3)

という２つの方程式が得られる。

ここで、古典的なハミルトン−ヤコビの偏微分方程式

　　　　　　　　　　　　　∂S_c／∂ｔ ＋(∇S_c)²／2m＋Ｖ＝0     （S_cは、ハミルトンの主関数）               (1.4)

と（1.2）を対比してみると、非常によく似た形であることがわかる。

そして、古典的な極限では(∇²R ／R)≈0となる(WKB近似)ことから、S_c＝Sを仮定すると、(1.2)は古典的な極限で(1.4)になるものと考えられる。なお、古典的なハミルトン−ヤコビの偏微分方程式で成り立つp＝∇S_cより、

　　　　　　　　　　　　　p＝∇S　　　　（p：運動量）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(1.5)

も成り立つ。

これらのことより、(1.2)は量子力学的なハミルトン−ヤコビの偏微分方程式であると考えることができ、その違いは、

　　　　　　　　　　　　　Ｑ ＝−(1/2m)(∇²R ／R)                                               (1.6)

という項が加わるだけである。つまり、量子力学的なハミルトン−ヤコビの偏微分方程式(1.2)は、

　　　　　　　　　　　　　∂S／∂ｔ ＋(∇S)²／2m＋Ｖ＋Ｑ ＝0　　　　　　　　　　　　　　　　　　　　(1.7)

と表すことができる。(1.7)の形を見ればわかるように、Ｑは、外部ポテンシャルＶに付加されたポテンシャルであると考えることができ、このポテンシャルＱを量子ポテンシャルという。つまり、(1.6)が量子ポテンシャルの定義となる。

　一方、(1.3)であるが、(1.1)よりR²＝ΨΨ^*＝ρ(ρ：確率密度)であることと、(1.5)から、

　　　　　　　　　　　　　∂R²／∂ｔ ＋∇・(R²∇S／m)＝∂ρ／∂ｔ ＋∇・(ρp)＝∂ρ／∂ｔ ＋div(ρp)＝0          (1.8)

が成り立ち、これは確率密度についての、連続の方程式であると考えることができる。

　さて、(1.7)が量子力学的なハミルトン−ヤコビの偏微分方程式であるなら、必然的に運動方程式が成り立つはずである。これが、どのような意味を持つかは定かではないが、形式的に運動方程式を求めれば、

　　　　　　　　　　　　　mdv／dt＝−∇(Ｖ＋Ｑ)　　　(v：速度)　　　　　　　　　　　　　　　　　(1.9)

となる。

１．１．３　存在論的解釈の要約

　１．１．２による一群の数式の展開の結果について、ボームは次のような存在論的解釈を与えている。

�@　電子のような粒子は実際に存在し、連続な変化し、因果的に決定される明確な位置r(t)を有する。

�A　この粒子は、新しいタイプの量子的な場から常に作用され、決して離れることがない。そして、この量子的な場はRとS、
　　　もしくは、Ψ＝Rexp(iS) によって与えられる。この時Ψは、シュレディンガー方程式を満たすもので、それに従い、連続的に
　　　変化し、かつ因果的に決定される。

�B　粒子は運動方程式
　　　　　　　mdv／dt＝−∇(Ｖ＋Ｑ)
　　を持ち、このことは、粒子に作用する力は、古典的な力−∇Ｖだけではなく、量子的な力−∇Ｑ も加わることを意味する。

�C　粒子の運動量は、p＝∇Sに限定される。そして、量子的な場Ψが一価であることから

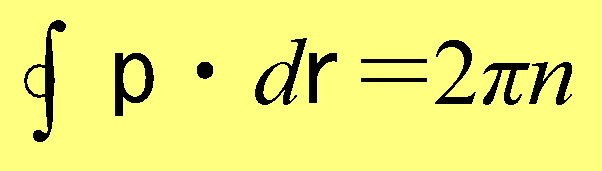　　　　　    （ 原子単位系であるいこと注意）                                 (1.10)

  が成り立つ。これは、ボーア−ゾーマフェルトの量子条件と似ている。

�D　粒子の統計的なアンサンブルでは、全て同じ量子的な場Ψが取られるため、確率密度はρ＝R²となる。また、初期条件が
　　 ρ＝R²であったなら、(1.8)により、ρ＝R²がずっと保たれる。

　これらのことから、粒子は量子的な場Ψ(「場の量子論」でいう量子場との混同を避けるため、あえて「量子的な場」と呼ぶことにする。）を常に伴っており、運動方程式(1.9)を介しその作用を常に受けていることがわかる。そして、量子的な場Ψはシュレディンガー方程式に従い発展する。いずれも、連続で因果的な変化であるため、粒子に明確な位置を定義でき、軌道を有するものと考えられる。つまり、観測の有無に関わらず粒子は粒子として存在し、明確な位置を持っているということになり、標準解釈とは全く異なる。

　これは、まるで決定論への回帰ではないかと錯覚するかも知れないが、そうではない。粒子が位置を有し、計算方法がわかっていても、不確定性原理によって初期条件が確定されないため、運動の予測は不可能であり決定論とはならない。なお、標準解釈で利用する統計的な概念は、存在論的解釈では因果的に決定される粒子軌道のアンサンブルにのみ適用されるものとなる。

　以上の存在論的解釈の内容は、ボームが最初に与えた、一先ずの要約である。これを出発として、さらに展開されることになる。

ボーム力学に戻る

ＴＯＰページに戻る

前に戻る　 次に進む