Ｐ(2,1)_ｃrａｌ＝Ｐ(経路１)＋Ｐ(経路２)＋Ｐ(経路３)＋・・・・

となるのに対して、量子的なケースでは位置１から位置２に伝播する確率振幅が、それぞれの経路を伝播する確率振幅の総和で、

　　                Ｇ(2,1)＝Ｇ(経路１)＋Ｇ(経路２)＋Ｇ(経路３)＋・・・・

となる。そして、これに対する確率は、

          Ｐ(2,1)_ｑｕａ＝ＧＧ^*＝|Ｇ(経路１)|²＋|Ｇ(経路２)|²＋Ｇ(経路１)Ｇ^*(経路２)＋Ｇ^*(経路１)Ｇ(経路２)＋・・・・

である。量子力学の特徴でもある干渉項(第３項、第４項）が生じるため、確率はそれぞれの経路の確率の総和にはならない。

  さて、このような量子的伝播関数に対して、定義を与えることとする。なお、ここでも古典的な場合と同様に伝播関数（以下、量子的伝播関数を単に「伝播関数」と呼ぶことにする）は、時間の差のみに依存することとする。これは、時間に依存しないハミルトニアンを扱う場合のみに有効な前提である。

(1.16)が量子的な伝播関数の定義であるが、Ｇの上付き添え字＋はt₂＞t₁を意味し、i は虚数で、便宜上付したものである。そして、この確率振幅に対応する確率は、

             Ｐ(r₂,r₁ ，t₂−t₁)＝Ｇ⁺(r₂ ,r₁ ，t₂−t₁)^*Ｇ⁺(r₂ ,　r₁ ，t₂−t₁)

となる。ここで注意すべきこととして、ｒ₁の粒子とｒ₂の粒子は同種の粒子なら何でもよく、同一の粒子であると考える必要はない。電子の中のどの電子というように区別することは量子力学では、意味をなさないからである。なお、(1.16）で定義されたＧ⁺は、遅延伝播関数とも呼ばれ、t₂≦t₁では０になる。逆に、t₂≧t₁で０となる、先進伝播関数と呼ばれるものもあり、これは反粒子やホールの確率振幅を記述するのに用いられる。

  さて、より正確には「位置r₁に粒子がある」というのは粒子が、δ(r - r₁)という位置固有状態にあるというべきであるが、これを任意の固有状態状態φ_k(r) に一般化し次のように定義することができる。

  また、位置固有状態の場合と同様にiＧ⁺(k₂,k₁ ，t₂−t₁)_t2≦t1＝０である。

　次に、自由伝播関数を計算してみる。
　時間t₁に自由粒子の状態がφ_k1(r)であるとすると、その波動関数は、

                            ψ(r ，t₁）＝φ_k1(r)　　　　　　　　　　　　　　　　　　　　　　　　　　(1.18)

　となる。その後、シュレディンガー方程式により時間t２での波動関数は、

　　　　　　　　　　 　       ψ(r，t₂）＝φ_k1(r)ｅｘｐ(−iεk₁(t₂−t₁))　　　　　              　　　　(1.19)

となる。ここで、εk₁は状態φ_k1(r)における粒子のエネルギーである。

以上により、時間t₂に状態φ_k2(r)　に粒子が存在する確率振幅を求めると、

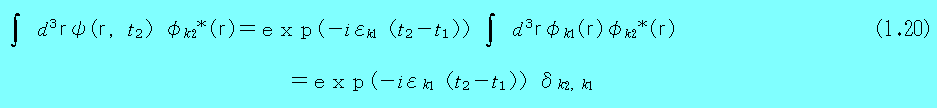
となる。
　よって、iＧ⁺(k₂ ,　k₁  ，t₂−t₁)の定義から
　　　　　　　Ｇ₀⁺(k₂ ,　k₁  ，t₂−t₁)＝−iθ_t2−t1ｅｘｐ(−iεk₁(t₂−t₁))δ_k2,k1
　　　　　　　　　　　　　　　　　　＝δ_k2,k1Ｇ₀＋(k₂ ,t₂−t₁)　　　　　　　　　　　　　            　　(1.21)
となる。

　ここで

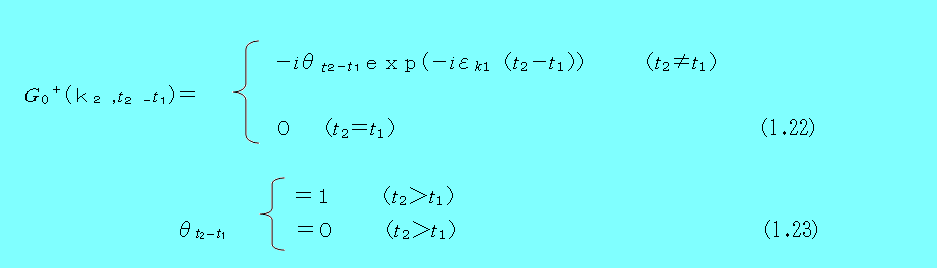
次に、古典的伝播関数と同様にフーリエ―変換を用いて、t をωに変換する。ここで、エネルギーのパラメーターである振動数となる。まず、

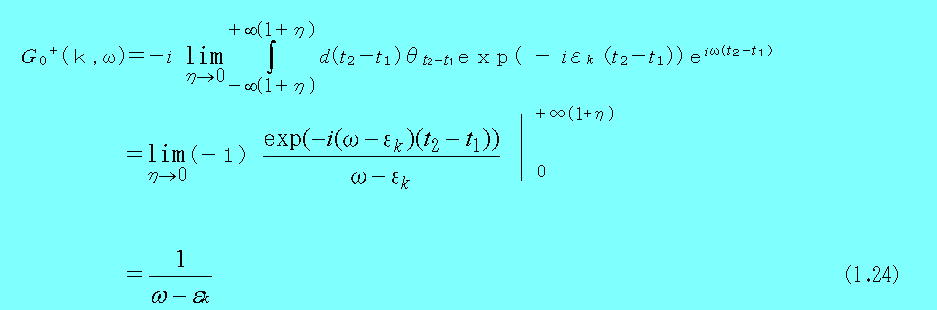
となる。ここで、ηは正無限小数あり、(1.24)は積分範囲に正無限小数があるためフリーエー変換とは異なる。そこで、この正無限小数を用いて、Ｇ^₀+(k ，t₂−t₁)の定義を若干修正する。

　　                    　Ｇ₀⁺(k ，t₂−t₁)＝−iθ_t2−t1ｅｘｐ(−i(ε_k1−iη)(t₂−t₁))　　　　　　                 (1.25)

　
とすればよい。

そして、(1.24)はｌｉｍを用いることなく、

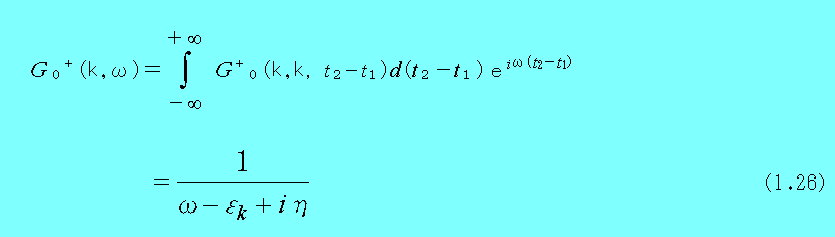
とフーリエ―変換で表すことができる。

  さて、(1.26)の極ではω＝ε_k が成り立っているが、これはエネルギーと振動数の関係に他ならない。（＝１としている）この関係は偶然ではなく、一般的に次のことが言える。

(1.26)では、τ＝∞でありその状態はずっと保たれたままとなる。自由粒子であることから当然である。

次に進む　１つ前に戻る

「場の量子論」に戻る

ＴＯＰページに戻る