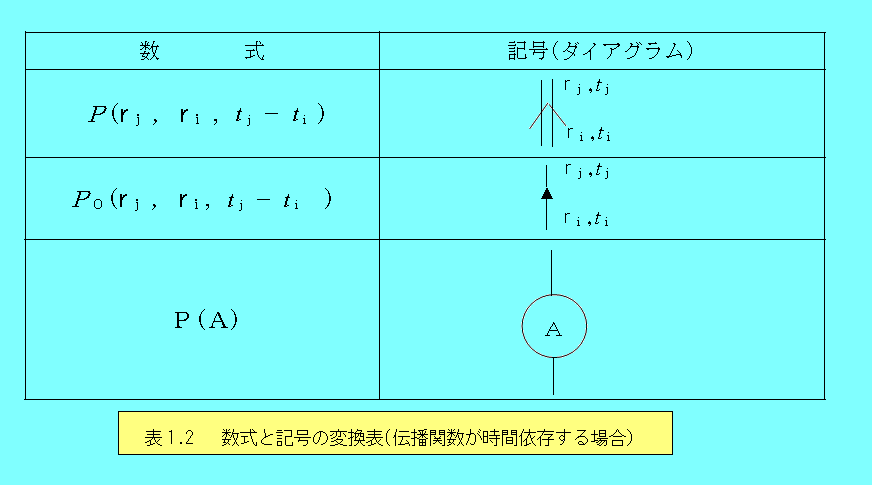
時間に依存する伝播関数
これまでの考察を、時間に依存する伝播関数P(rj,ri,tj−ti)に拡張する。ここで、tj−tiと記述したのは、散乱が時間に依存しない場合、伝播関数は時間の差のみに依存することによる。
P0(rj,ri,tj−ti)を、時間tiにriにあった粒子が散乱を受けずに、時間tjにriに達する確率とする。このような、散乱を受けない運動の伝播関数を自由伝播関数という。また、P(A)を散乱点と粒子の相互作用を表すものとし、考察を単純化するため、この相互作用は散乱点に粒子が達すると瞬時に生じるものとする。
まず、伝播関数が時間依存する場合に、数式と記号(ダイアグラム)の変換表を拡張させると表1.2のようになる。なお、ダイアグラムを描く際には、y方向を時間が増加する方向にとることとする。

そして、これを用いてダイアグラムを描くと次のようになる。
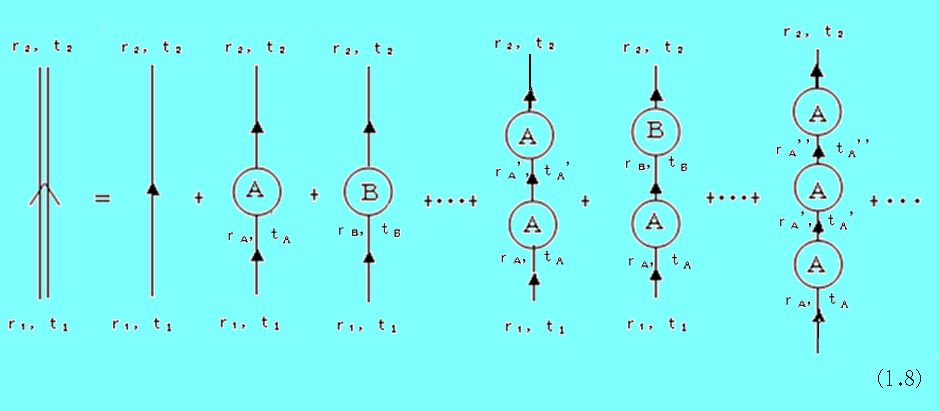
ここで、散乱点Aで散乱が起こる時間tAという時間は、t1とt2の間のある瞬間であり、決められていないことに注意しなければならない。例えば、時間t1にr1にあった粒子が、散乱点Aで1回散乱を受け、時間t2にr1にある確率を計算するには、t1とt2の間のすべての時間tAで散乱が起こる確率を重ね合わせなければならない。(式(1.9))
P((r1, t1)→A→(r2,t2))=  dtAP0(rA,r1,tA− t1)P(A)P0(r2,rA,t2−tA)
(1.9)
dtAP0(rA,r1,tA− t1)P(A)P0(r2,rA,t2−tA)
(1.9)
従って、(1.8)を数式で表すと、次のようになる。
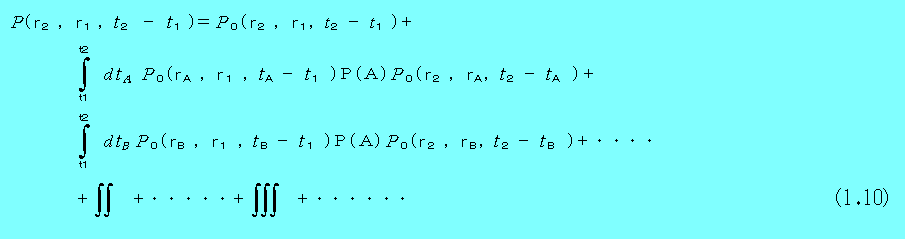
このように記述すると多重積分がたくさん現れ、計算が困難なように思われるが、フーリエ―変換を用いることにより、簡単な積に置き換えることができる。
P0(rj,ri ,tj− ti)をフーリエ―変換を用いて表すには、
P(rj,ri ,tj − ti )=0 (tj ≦ ti) (1.11)
を伝播関数の定義として加えと便利である。これにより、(1.12)のように表すことができる。
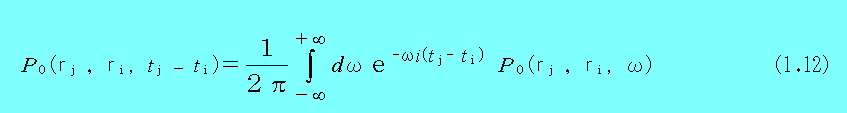
すると
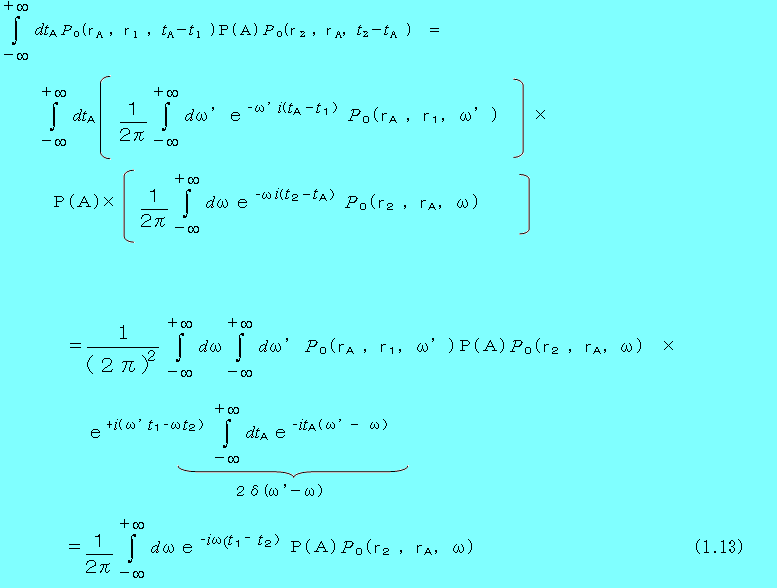
となる。従って、このような積分を(1.10)のすべての項について行い、最終的に逆フーリエ―変換すると、
P(r2,r1 ,ω)=P0(r2 , r1 ,ω)+P0(rA , r1 ,ω)P(A)P0(r2,rA ,ω)+・・・ (1.14)
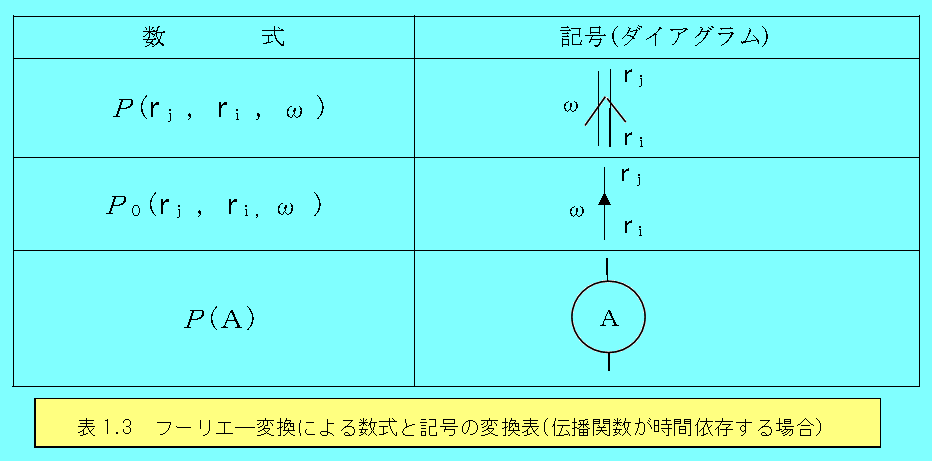
となる。このように、時間に依存する伝播関数についても、フーリエ―変換を用いることで式(1.1)と同じくらい簡単に表すことができる。さらに、数式と記号の変換表もフーリエ―変換による場合に書き換えることができ、表1.3のようになる。
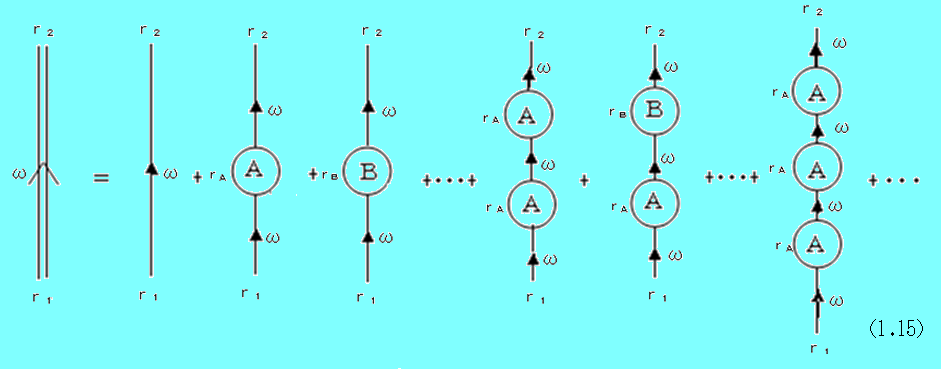
そして、(1.8)は(1.15)のように描かれる。
TOPページに戻る「場の量子論」に戻る