ダイアグラムの導入

 

　ここからは、少し話を抽象化し、「ピン」を「散乱点」、「玉」を「粒子」、ピンボールゲームを「系」と呼ぶことにする。もし、抽象的で物理的イメージが掴みにくくなった場合には、図1.2.2に立ち返って考えてもらいたい。

 

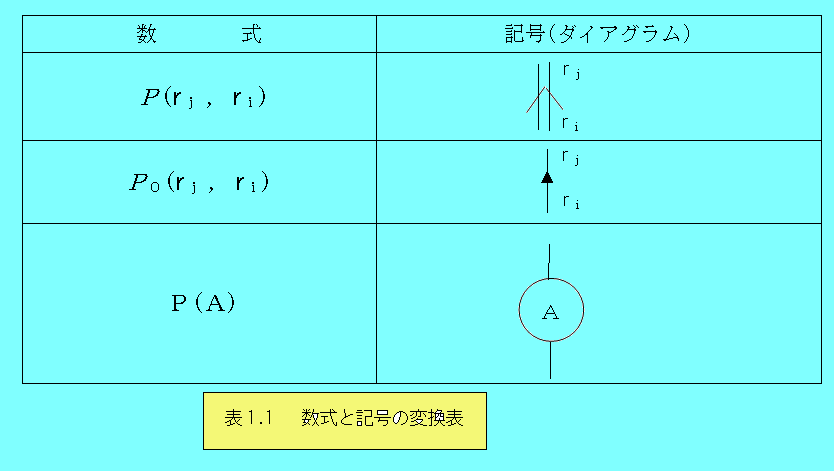
　さて、式(1.1)を簡単に理解するために、ダイアグラムを用いることにする。表1.1は、式(1.1）のような式をダイヤグラムに変換したり、逆にダイアグラムから数式に変換するための表である。

 

QUANTMUFIELD-1-3.1.1IM.PNG - 17,059BYTES

 

この変換表により、(1.1）をダイアグラムにすると、

 

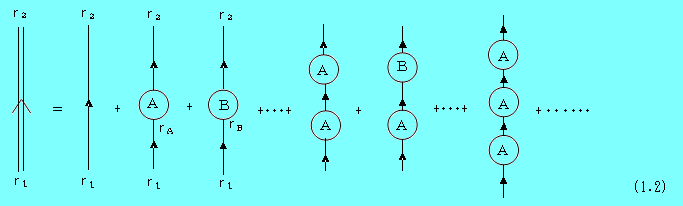
QUANTMUFIELD-1-3.S1.2IM.PNG - 9,513BYTES 

となる。当然のことながら、式(1.1)と(1.2)は完全に等しい。しかしダイアグラムでは、粒子が散乱点の連なりから散乱を受けつつr1からr2に運動する様子が描かれており、数式よりも理解しやすい。

 

次に、Ｐ(r2,r1)の大きさを実際に計算してみよう。まず、

                   Ｐ(Ａ)≠０

　　　             Ｐ(Ｂ)＝Ｐ(Ｃ)＝Ｐ(Ｄ)＝Ｐ(Ｅ)＝Ｐ(Ｆ)＝０　　　　　　　　　　　　　　　　　　　（1.3)

 

のケースについて考えてみる。式(1.1)を使った場合は、

             

              Ｐ(r2,r1)＝Ｐ0(r2,r1)＋Ｐ0(rA,r1)Ｐ(Ａ)Ｐ0(r2,rA)＋

　　　　　　　　        Ｐ0(rA,r1)Ｐ(Ａ)Ｐ0(rA,rA)Ｐ(Ａ)Ｐ0(r2,rA)＋

                        Ｐ0(rA,r1)Ｐ(Ａ)Ｐ0(rA,rA)Ｐ(Ａ)Ｐ0(rＡ,rＡ)Ｐ(Ａ)Ｐ0(r2,rA)＋・・・・　　　　　　

                      ＝Ｐ0(r2,r1)＋Ｐ0(rA,r1)Ｐ(Ａ)Ｐ0(r2,rA)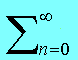SIGN0MUGEN.PNG - 566BYTES (Ｐ(Ａ)Ｐ0(rA,rA))n

　　　　　　　        ＝Ｐ0(r2,r1)＋Ｐ0(rA,r1)Ｐ(Ａ)Ｐ0(r2,rA)／（１−Ｐ(Ａ)Ｐ0(rA,rA)）　　　　　　(1.4)

 

 

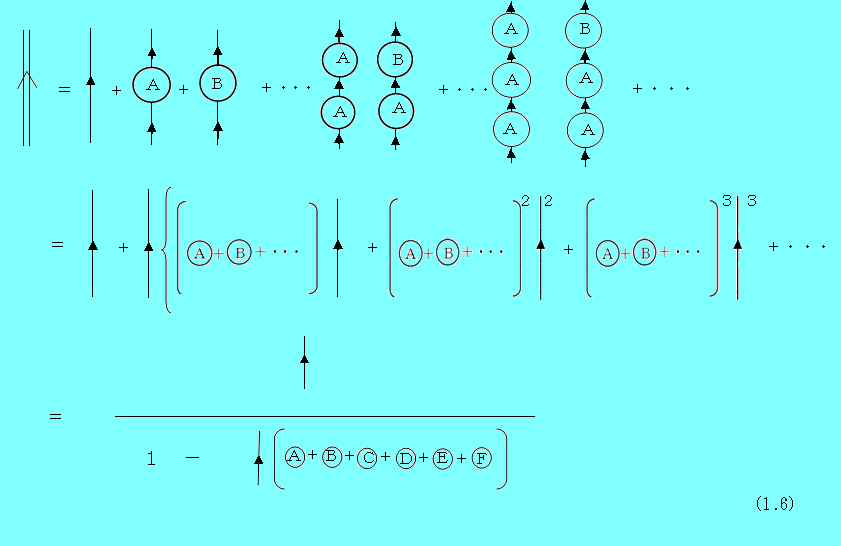
  式(1.2)と表1.1を用いて求めてみると、次のようになる。

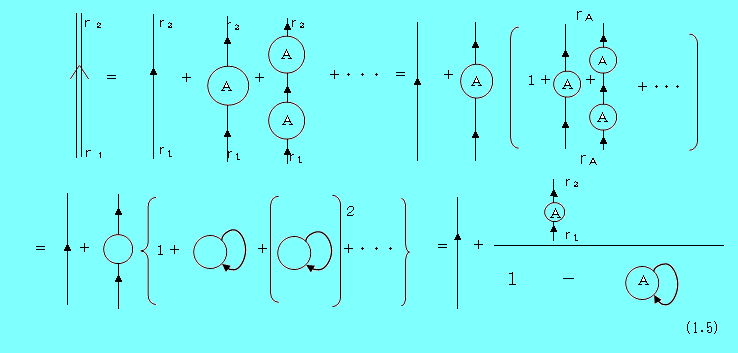
QUANTMUFIELD-1-3.S1.5IM.PNG - 19,012BYTES

   次に、散乱の無い伝播関数が全て同じケース（Ｐ0(ri,rj)＝ｃ）について求めてみる。式(1.1)を使った場合は、

                 Ｐ(r2,r1)＝ｃ＋ｃ2(Ｐ(Ａ)＋Ｐ(Ｂ)＋Ｐ(Ｃ)＋Ｐ(Ｄ)＋Ｐ(Ｅ)＋Ｐ(Ｆ))

　　　　　　　　　＋ｃ3(Ｐ(Ａ)＋Ｐ(Ｂ)＋Ｐ(Ｃ)＋Ｐ(Ｄ)＋Ｐ(Ｅ)＋Ｐ(Ｆ))2

　　　　　　　    ＋ｃ4(Ｐ(Ａ)＋Ｐ(Ｂ)＋Ｐ(Ｃ)＋Ｐ(Ｄ)＋Ｐ(Ｅ)＋Ｐ(Ｆ))3＋・・・・・・

　　　　　　　   ＝ｃ／{１−ｃ(Ｐ(Ａ)＋Ｐ(Ｂ)＋Ｐ(Ｃ)＋Ｐ(Ｄ)＋Ｐ(Ｅ)＋Ｐ(Ｆ))}

となる。

 

   続いて、式(1.2)と表1.1を用いて求めてみる。

QUANTMUFIELD-1-3.S1.6IM.PNG - 30,151BYTES

   最後に少し変わったケースとして、

 

                       Ｐ(Ａ)＝Ｐ(Ｂ)＝Ｐ(Ｃ)＝Ｐ(Ｄ)＝Ｐ(Ｅ)＝Ｐ(Ｆ）≦1/10

　　　　               Ｐ0(r2,r1)≒1／2　　　　　　　　　　　　　　　　　　　　　　　     （1.7)

 

について求めてみる。この場合は、散乱は多くても１回程度しか起こらないため、

 

            Ｐ(r2,r1)≒Ｐ0(r2,r1)＋Ｐ0(rA,r1)Ｐ(Ａ)Ｐ0(r2,rA)＋Ｐ0(rB,r1)Ｐ(Ｂ)Ｐ0(r2,rB)

　　　　　　　      ＋Ｐ0(rC,r1)Ｐ(Ｃ)Ｐ0(r2,rC)＋Ｐ0(rD,r1)Ｐ(Ｄ)Ｐ0(r2,rD)

　　　　　　　      ＋Ｐ0(rE ,r1)Ｐ(Ｅ)Ｐ0(r2,rE)＋Ｐ0(rF,r1)Ｐ(Ｆ)Ｐ0(r2,rF)

 

となる。これは、1オーダーの近似計算であり、同様にして、散乱回数に応じて任意のオーダーの近似計算が可能となる。

 

 

次に進む　１つ前に戻る

「場の量子論」に戻る


ＴＯＰページに戻る