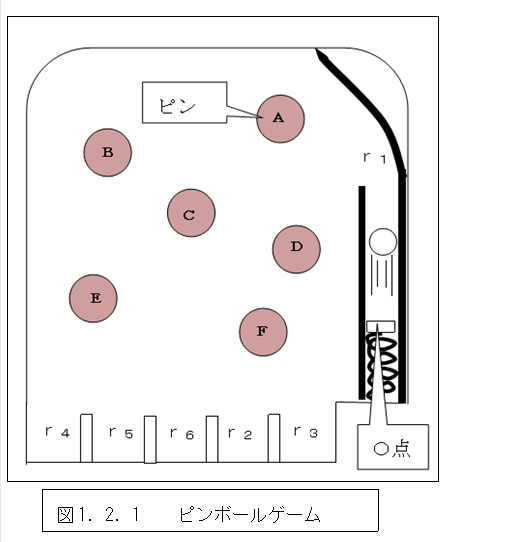
伝播関数のイメージをより明確にするために、確率振幅では無く確率を用いた伝播関数を考察する。このために、図1.2.1のようなピンボールゲームを用いることにする。
時間t1に玉がr1にがあり、ピンの間を散乱されながら通り、時間t2にr2に達する確率を、P(r2 ,t2 ,r1 ,t1 )と表す。
また、ピンにおける散乱は次のようなものとする。
(1)ピンAに玉が達した時に、散乱される確率をP(A)とし、錯乱されずに通り抜ける確率を1−P(A)とする。
(2)ピンAに散乱された後の玉の速度及び経路は、散乱される前の玉の速度及び経路には依存しない。
考察を簡単にするために、時間を考慮しないものとし、玉がr1の位置からあった場合に、最終的に静止する位置がr2である確率P(r2,r1)のみを考える。確率の定義から、P(r2,r1)は玉がr1からr2に至るあらゆる経路の確率の和となる。
例えば、どのピンからの散乱も受けることなく、直接r1からr2に運動することもあれば、r1からピンCまで移動し、ピンCによって散乱されr2に移動することもある。さらに、r1からピンBまで移動し、ピンBで散乱されピンFに移動し、ピンFでも散乱されr2に移動にしたり、あるいは、r1からピンDまで移動し、ピンDで散乱を2回受けr2に移動にする等、あらゆる経路の確率の和がP(r2,r1)である。
では、このP(r2,r1)を実際に求めることを考える。最も単純なのは、どのピンからの散乱も受けることなく直接r1からr2に運動する経路である。この経路の確率をP0(r2,r1)とする。(なお、この経路は必ずしも直線ではないことに注意。散乱を受けないあらゆる経路の和となる。)
次に、ピンAに散乱された後に、r2に達する確率を考えてみる。まず、r1からピンAまで散乱されず運動する確率は
P0(rA,r1)であり(rAはピンAの位置)、ピンAで散乱される確率はP(A)である。その後、ピンAから散乱されずにr2に達する確率は、P0(r2,rA)であるから、ピンAに散乱された後に、r2に達する確率=P0(rA,r1)P(A)P(r2,rA)となる。同様にして、
ピンBに散乱された後に、r2に達する確率=P0(rB,r1)P(A)P0(r2,rB)
ピンCに散乱された後に、r2に達する確率=P0(rC,r1)P(A)P0(r2,rC)
ピンDに散乱された後に、r2に達する確率=P0(rD,r1)P(A)P0(r2,rD)
・
・
である。
散乱は1回とは限らず、2回起こることもある。その場合は、
ピンAに2回散乱された後に、r2に達する確率 =P0(rA,r1)P(A)P0(r2,r2)P(A)P0(r2,rA)
ピンAに散乱された後、ピンBに散乱されr2に達する確率=P0(rA,r1)P(A)P0(rB,rA)P(B)P0(r2,rB)
ピンAに散乱された後、ピンCに散乱されr2に達する確率=P0(rA,r1)P(A)P0(rC,rA)P(C)P0(r2,rC)
ピンAに散乱された後、ピンDに散乱されr2に達する確率=P0(rA,r1)P(A)P0(rD,rA)P(D)P0(r2,rD)
・
・
・
である。
さらに散乱は1回2回のみならず何回でも起こることがあり、これらすべての項を足しあげたものが、P(r2,r1)となる。
P(r2,r1)=P0(r2,r1)+P0(rA,r1)P(A)P0(r2,rA)+P0(rB,r1)P(B)P0(r2,rB)
+・・・+P0(rA,r1)P(A)P0(rA,rA)P(A)P0(r2,rA)+P0(rA,r1)P(A)P0(rB,rA)P(B)P0(r2,rB)+・・・・・
(1.1)