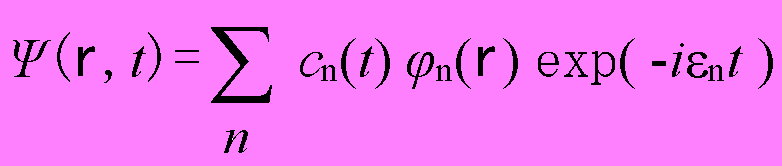まず、ハミルトニアンＨ₀があり、その固有関数φ_kと固有値ε_kがわかっており、φ_kは完全規格直交関数系であるとする。

　　　　　　　　　　　　　　　　Ｈ₀φ_k＝ε_kφ_k                  (1.1)

　初期状態として、系はφ_p状態にあるものとし、時刻t₁に摂動ポテンシャルＶ(r)が生じるものとする。すると、系のハミルトニアンは、Ｈ＝Ｈ₀＋Ｖとなり、状態もΨ(r,t)に変化し、これは次のシュレディンガー方程式に従う。

　　　　　　　　　　　　　　　　i∂Ψ(r,t)／∂ｔ　＝(Ｈ₀＋Ｖ )Ψ(r,t)                                 (1.2)

そして、φ_kの完全性によりΨ(r,t)は、

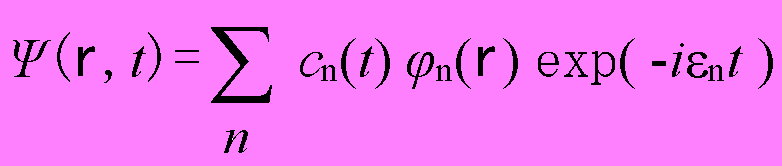                                                                  (1.3)

と表すことができる。これを、(1.2)に代入すると

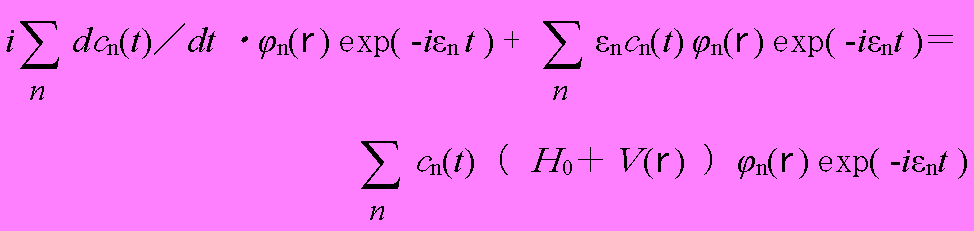                           　　          (1.4)

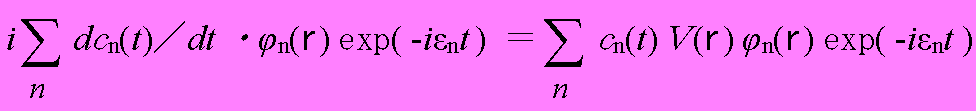                                              (1.5)

となる。

　ここで、(1.5)の両辺に対し、φ_p^(ｒ)との内積（φ_p^(ｒ)との積をとり、体積分 ^_∫d3rを求める）と、φ_p^(ｒ)が規格直交関数であることから

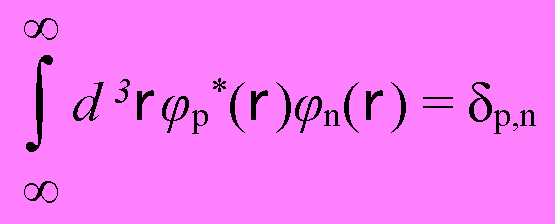                                                                           　 　　 (1.6)

が成り立ち、

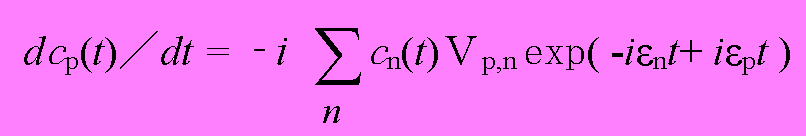                                                             (1.7)

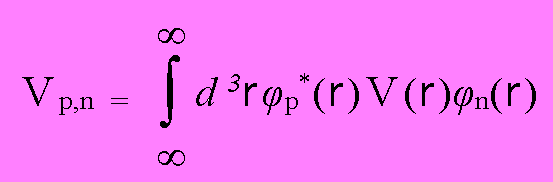                                                                       (1.8)

となる。

　摂動展開は、通常はこのように導かれる。なお、ここまでは近似計算ではなく、(1.7)は厳密解である。

　さて、初期条件として、時間t<t₁間は無摂動であり、c_n(t)=δ_n,sであるとする。つまり、t<t₁における系の状態がφ_sということである。そして、時間t＝t₁に摂動ポテンシャルＶ(ｒ）が生じるものとし、その後の時間t₂（t₂>t₁）における系の状態について考察する。

　ここで、摂動ポテンシャルを次のような、Ｖ'(r,t)に変更する。

　　　　　　　　　　Ｖ'(r,t)＝Ｖ(r)δ(t - t⁽¹⁾)      (t₂ > t⁽¹⁾  > t₁)

つまり、時間t₁とt₂の間にあるt⁽¹⁾でのみ、摂動ポテンシャルがＶ(ｒ)作用することになる。この場合、(1.7)は簡単に積分することができ、

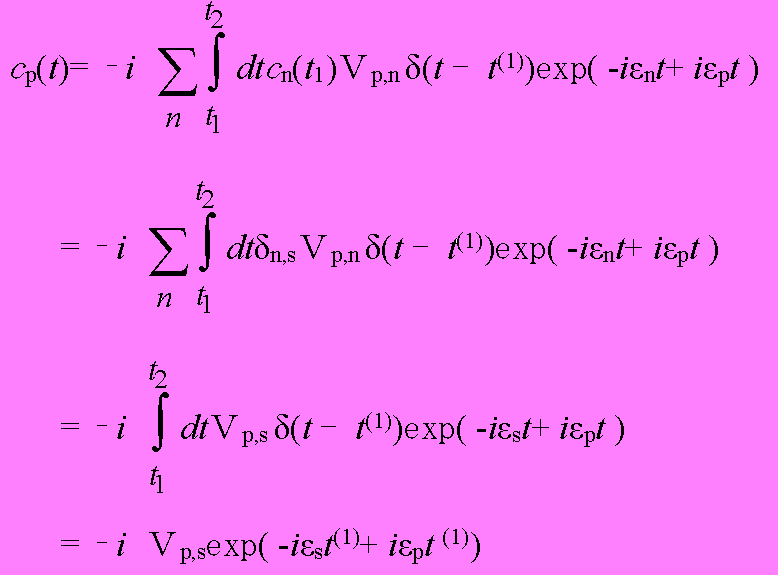                                                            (1.9)

となる。さて、摂動ポテンシャルは時間t₁とt₂の間にあるt⁽¹⁾という瞬間のみ働いたのであるから、これは摂動ポテンシャルにより１回だけ散乱を受けたことに相当する。そして、t₁⁽¹⁾ は t₁とt₂の間のある時間であるから、これらを重ね合わせることにより、１回だけ散乱を受ける場合の振幅c_P(1)(t₂)が、次にように求まる。

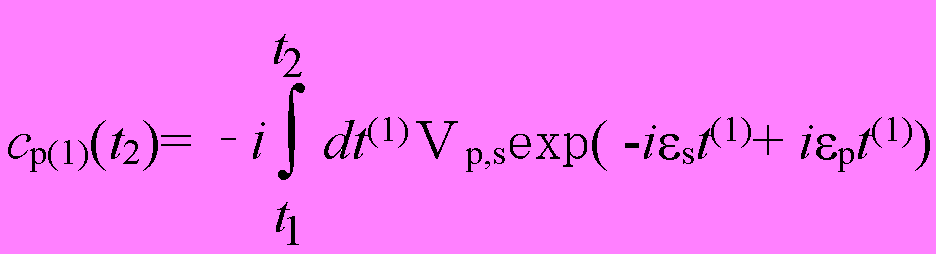                                                (1.10)

　続いて、今度は摂動ポテンシャルにより２回散乱を受ける場合について、求めてみる。この場合、次のような摂動ポテンシャルによる摂動が続けて起こるものとして求めればよい。

　　　　　　　　　　　　　Ｖ'(r,t)＝Ｖ(r)δ(t - t⁽²⁾)    (t₃> t⁽²⁾  > t₂)　　　　　　　　　　　　　　　　　(1.11)

　つまり、初期条件として、時刻t₂において各成分の振幅は(1.10)のようになっており、この状態から(1.11)のような摂動ポテンシャルが発生した場合に、t₃におけるc_pを求めるのである。再び(1.7)を用いて、

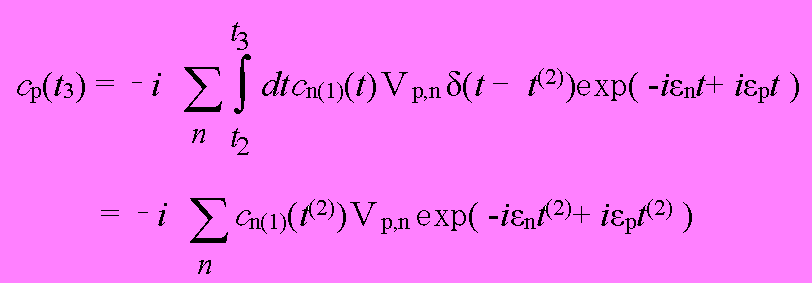                                       (1.12)

となる。さて、ここで再びt⁽²⁾について(1.9)のように重ね合わせととるのだが、同時にt₂についても重ね合わせをとる必要があるため、いわゆる畳み込み積分となり、積分範囲はt₁からt₃とする必要がある。よって、t₁とt₃の間で２回散乱を受ける場合の確率振幅c_p（2）(t₃)は、

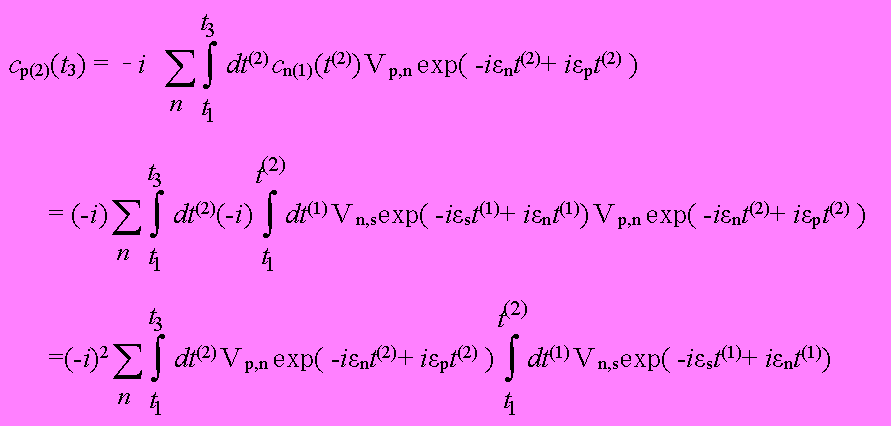                                 (1.13)

となる。

　さて、こうなると３回散乱を受ける場合、４回散乱を受ける場合・・・・と順次計算することで何回も求めることができるのがわかる。表現を簡単にするため、

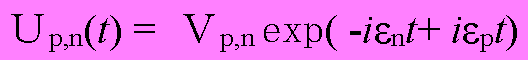                                                           (1.14)

と表わすと、

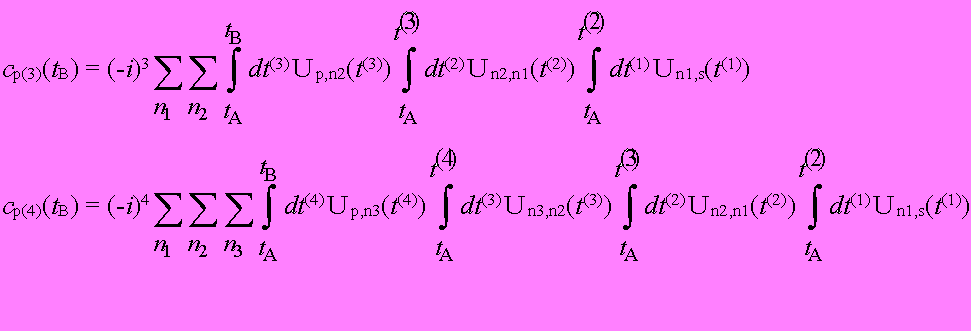              (1.15)

となる。（時間は,初期状態をt_A,終状態をt_Bとした。）

ここで、散乱回数については０回(状態が変化しない、δ_p,s)から１回、２回、３回・・・か無限回まであることが考えられるため、すべての重ね合わせを取ることとする。そうすると、初期状態がφ_sであった場合のc_P(t)は、

　　　　c_P(t)＝δ_p,s＋c_p（1）(t)＋c_p（2）(t)＋c_p（3）(t)＋c_p（4）(t)＋c_p（5）(t)＋c_p（2）(t)＋・・・・・・・・・　　　　　　(1.16)

となる。さて、この(1.16)は通常の摂動展開と同じものであり、n次の摂動c_p^（n）(t)との関係は、

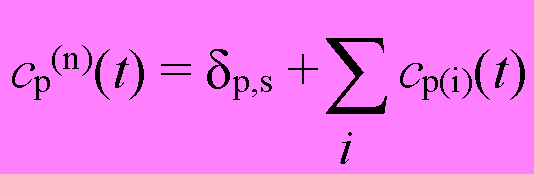                                                                   (1.17)

である。

　このことから、逆にいえば、摂動展開とは、無摂動な状態に作用する摂動ポテンシャルを、作用する回数によって分解するものであり、摂動展開による近似とは、摂動ポテンシャルが無摂動状態に作用する回数を有限回として近似するものであるということがいえる。

量子力学に戻る

ＴＯＰページに戻る