古典的なピンボールゲームから出発して、そのアナロジーにより直感的に理解しやすい方法で伝播関数を説明して来たが、ここでこれまでの議論を裏付ける証明を与える。古典的ケースで、各経路を通る確率の和が伝播関数になるというのは、古典的伝播関数は伝播する確率を表していることから、確率の和の法則より明らかである。これまでの議論は、これを確率振幅にまで拡大適用し展開したものである。従って、この拡大適用が正しいものであったかが、明らかではないのなら議論は砂上の楼閣である。
　

　まず、伝播関数はシュレディンガー方程式のグリーン関数であるということを出発点とする。すなわち、ポテンシャルが無い場合については、

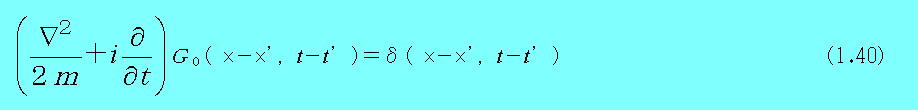
を満たすＧ₀である。ここで、Ｇ₀をフーリエー変換で

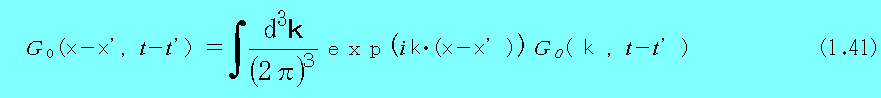
と与え、(1.40)に代入すると

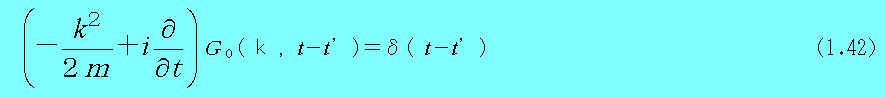
となる。

  ここで、(1.41)のＧ₀を(1.42)に代入すると、(1.42)の解であり、Ｇ₀がシュレディンガー方程式のグリーン関数であることが証明される。（dθ_x ／dx＝δ(x）及びｆ(x)δ(x)＝ｆ(０)δ(x)を用いる）

　同様にして、(1.29)のようなポテンシャルＶ(∇)がある場合のシュレディンガー方程式のグリーン関数Ｇを与えると、

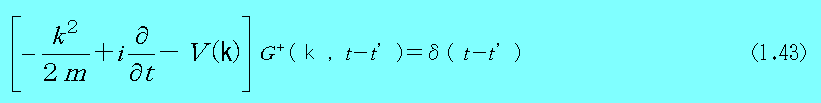
となる。ここで Ｖ(k)は、Ｖ(∇)のフーリエー変換である。この解は、積分方程式(1.44)となり、

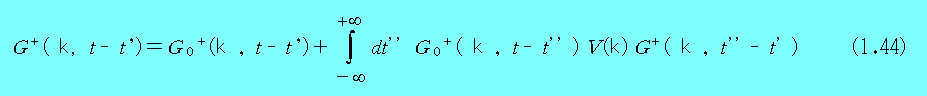
(1.44)を(1.43)に代入し、(1.42)を用いると

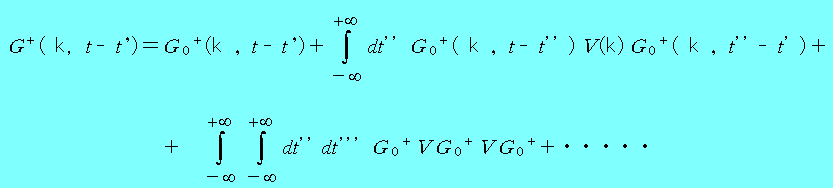 (1.45)

となる。これは、(1.34)と同じ結果である。

　これにより、ピンボールゲームのアナロジーから摂動展開により求めた伝播関数と、シュレディンガー方程式から求めた伝播関数が一致することが証明された。逆に言えば、シュレディンガー方程式から数学的に伝播関数を求めた場合、その物理的イメージはピンボールゲームのようなものであり、散乱体に散乱されなかった場合、１回散乱された場合、２回散乱された場合、３回散乱された場合、・・・・の確率振幅の和となっていることが理解できる。

１つ前に戻る

「場の量子論」に戻る

ＴＯＰページに戻る