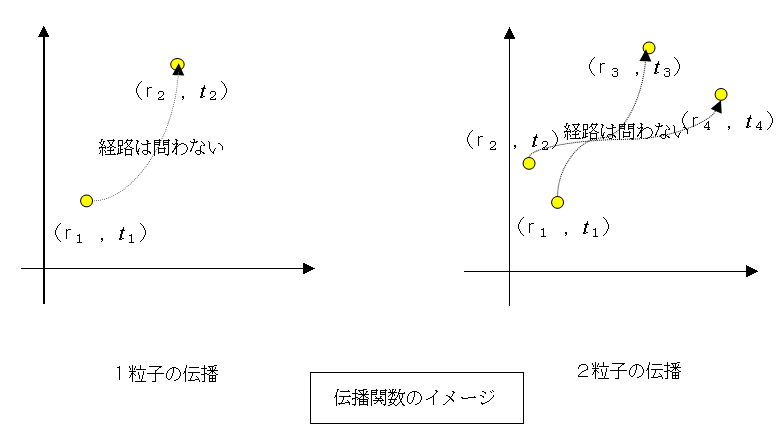
伝播関数(プロパゲーター)のイメージ
伝播関数は、グリーン関数でもあるが、これを計算することが場の量子論の第一歩と言っても過言ではない。しかし、定義から闇雲に計算しても一体何を計算しているのかが見えなくなってくる。そこで、まずは伝播関数の物理的イメージを捉えることから始める。
「ある系の中で、粒子Pが時間t1という瞬間に位置r1にあり、系の中の他の粒子や外部ポテンシャルとの相互作用を受けつつ、運動するものとする。その後、時間t2という瞬間に位置r2に粒子Pを観測する確率振幅を(1粒子系の)伝播関数という。」
これが、1粒子系の伝播関数の定義である。観測する確率であれば定義は単純明快であるが、確率振幅となっているところがわかりにくい。しかし、確率振幅はその二乗(複素共役との積)が存在確率を表すものであり、波動関数と考えて差し支えない。従って、「伝播」というのは、「伝わること」ということであり、粒子がある時ある位置から、別のある時ある位置に運動する(つまり「伝わる」)確率のようなものというのが、1粒子系における伝播関数のイメージである。
同様に、2粒子系の伝播関数の定義は「ある系の中に、粒子1が時間t1に位置r1
、粒子2が時間t2に位置r2にあった場合、一つの粒子を時間t3もう一つの粒子をt4に、それぞれ位置r3 、r4観測する確率振幅を2粒子系における伝播関数という。」となる。
なお、ここで粒子1と粒子2は全く同じ粒子であり、区別できないものとした。
さて、もう一つ重要なものとして、非伝播関数(ノンプロパゲーター)というものがある。
これは、伝播関数とは逆に「ある系の中で、粒子Pが時間t1という瞬間に位置r1にあり、その後、時間t2という瞬間に位置r2に粒子Pを観測しない確率振幅を(1粒子系の)非伝播関数という。」というものである。2粒子系においても、同様に定義される。

TOPページに戻る「場の量子論」に戻る