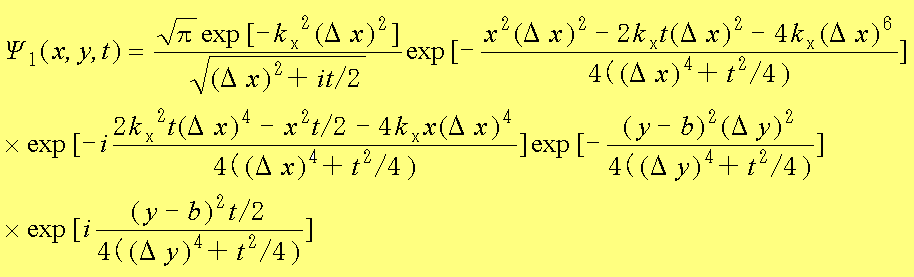 (1.45)
(1.45)ボーム力学
1.5 二重スリット1
1.5.1 ボームによる二重スリットの解釈
D.Bohmによる二重スリットの解釈は、De Broglieが提唱した「パイロット波」解釈を発展させたものである。そのような経緯もあり、「ドブロイ=ボーム解釈」と呼ばれることもある。なお、二重スリットの解釈と述べたが、それは量子力学の解釈そのものを意味している。このことは、『THE UNDIVIDED UNIVERSE』にも触れられている。
「「パイロット波」が粒子の運動を誘導するという考えは、1927年にDe Broglieによって初めて主張されたが、それは単粒子系のみによるものであった。De Broglieは、1927年に開催された「ソルベイ会議」でこの考えをプレゼンしたが、Pauliによって激しく批判された。Pauliの最も重要な批判は、二体の散乱過程では、このモデルを矛盾無く適用できないということであった。その結果、De Broglieは自分の主張を放棄した。「パイロット波」の考えは、その後1952年に、D.Bohmによって多体系での解釈が加えられ、再び主張された。De Broglieの主張は、Pauliの批判に答えることが可能であり、実際に、量子現象の多くの領域に適用できる観測の理論を含む一貫した解釈に道を開いた。その結果、De Broglieは最初の自分の考えを再度主張し、それらを多様な方法で発展させていった。」(『THE UNDIVIDED UNIVERSE』より抜粋)
さて、「ドブロイ=ボーム解釈」による二重スリットの解釈は、おおまかにいって次のようなものである。例として、電子を用いて二重スリットの実験を行うものとした。なお、二重スリットについて詳しく知らない人は、http://ja.wikipedia.org/wiki/%E4%BA%8C%E9%87%8D%E3%82%B9%E3%83%AA%E3%83%83%E3%83%88%E5%AE%9F%E9%A8%93(ウィキペディア)等を参照してください。
①電子は粒子として存在している。
②波動関数は、粒子の運動を誘導する量子的な場である。
③電子は粒子として、量子的な場によって誘導され運動する。
④電子は粒子だから、二重スリットのどちらか一方を通り抜ける。
⑤量子的な場は、二重スリットの両方を通り、通り抜けると干渉を起こす。
⑥電子は粒子として、量子的な場によって誘導されるから、二重スリットを通り抜けると干渉した量子的な場によって誘導される。
⑦その結果、スクリーンに浮かび上がる電子の像は干渉した波のようなものになる。
標準解釈では、粒子の実在を前提とせず、実在の基礎を波動関数とするため、波動関数が同時に2つのスリットを通り抜け干渉を起こし、その結果スクリーン上に干渉像のような分布が浮かび上がるということになるであろう。古典的には理解しにくいが、粒子の実在を否定するため、波動関数が同時に2つのスリットを通り抜けることができるというロジックだ。
標準解釈がどうであれ、ボーム力学では波動関数が粒子の運動を誘発する量子的な場となる。従って、ボーム力学で二重スリットを扱うには、
①二重スリットの波動関数を求める。
②求めた波動関数Ψ(r,t)を、式(1.1) Ψ(r,t)=Rexp(iS) に当てはめ、RまたはSを求める。
③Sを求めた場合、式(1.5)p=∇Sから運動量pが求まり、ここから粒子運動の軌道が求まる。ただし、初期条件を確定させることができないため、初期条件を仮に設定した場合の軌道となる。
④Rを求めた場合、式(1.6)Q =-(1/2m)(∇2R /R) から量子ポテンシャルQが求まり、これを式(1.9) mdv/dt=-∇(V+Q)に代入すれば、粒子運動の軌道が求まる。ただし、初期条件のうち初速度は③から求まるが、位置のほうは確定させることができないため、やはり初期条件を仮に設定した場合の軌道となることは、③の場合と同様である。
とすればよく、ここでは③を用いることとする。
1.5.2 2次元ガウス波束
まず、t=0で中心がx=0,y=bにあり、x方向に速度kxで移動するガウス波束の波動関数を求めてみる。x方向とy方向はそれぞれど独立であるため、前節の式(1.29)より直ちに、
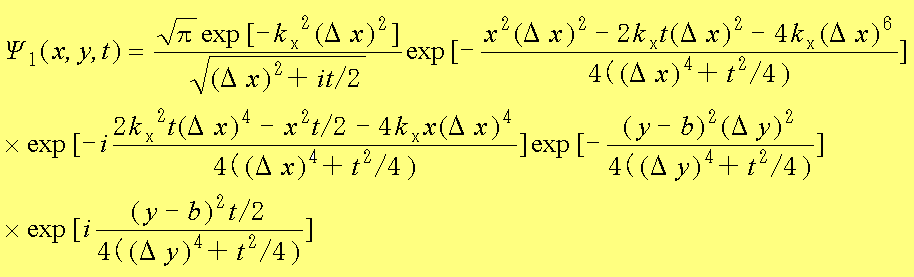 (1.45)
(1.45)
となる。なお、Δyはy方向の位置の不確かさである。また、m=1としている。
同様にして、t=0で中心がx=0,y=-bにあり、x方向に速度kxで移動するガウス波束の波動関数を求めてみると、
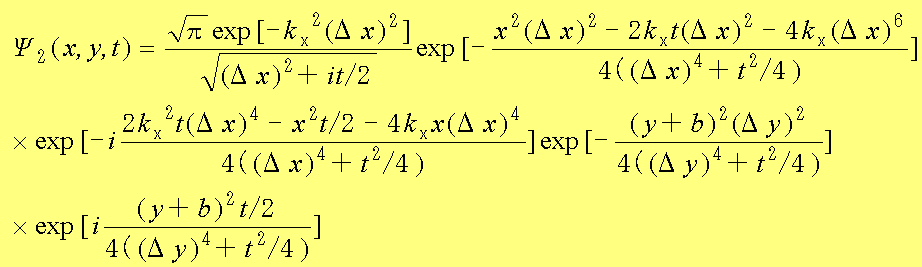 (1.46)
(1.46)
となる。
Ψ1とΨ2は、いずれもx方向に速度kxで進行するガウス波束であるが、時間t=0での波束の中心はそれぞれ(0,b)(0,-b)となっている。図にすれば図1.5.1のような関係であり、二重スリットによる波動関数の干渉とよく似た状況である。
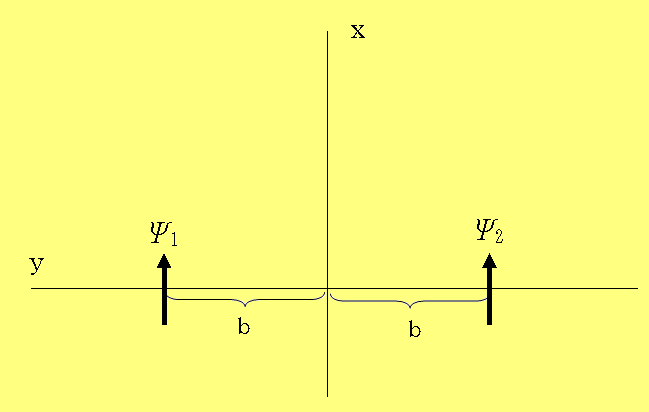
図1.5.1
そこで、Ψ1とΨ2を重ね合わせたものを二重スリットの波動関数であると考え、Ψ1+Ψ2を求めてみる。
まず、x方向y方向のガウス波束がそれぞれ独立であるため当然のことであるが、(1.45)と(1.46)から直ちにわかることは、xに依存する因子はΨ1 ,Ψ2ともに共通である。そこで、これをg(x)とすれば、
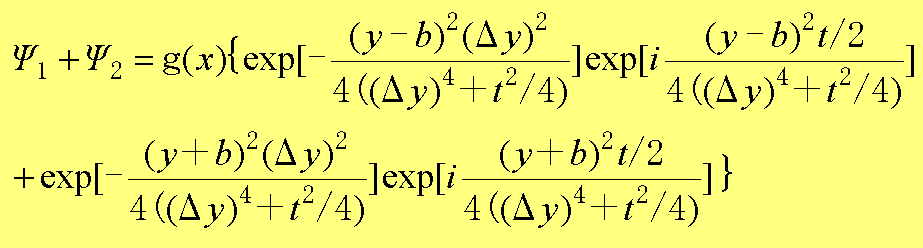 (1.47)
(1.47)
となる。ここで、σy=4((Δy)4+t2/4)として整理すれば、
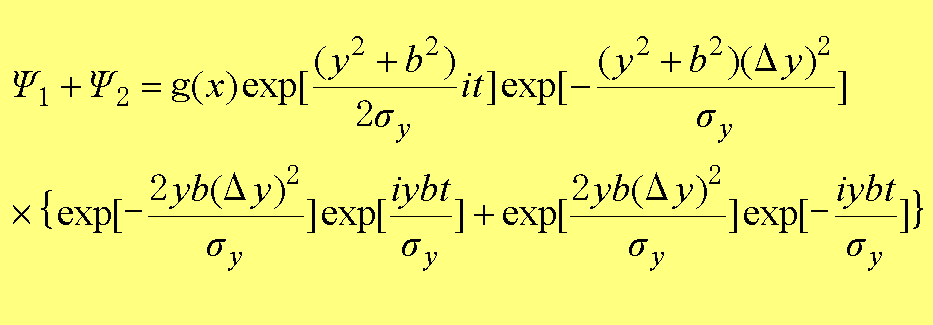 (1.48)
(1.48)
となる。さらにA=2b(Δy)2/σy ,B=bt/σyとすれば、
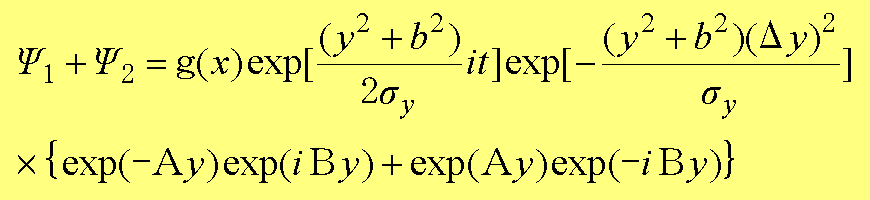 (1.49)
(1.49)
となる。ここで、式(1.49)の{・・・}をrexp(iθ)とおけば、
r={exp(2Ay)+exp(-2Ay)+2cos(2By)}1/2 (1.50)
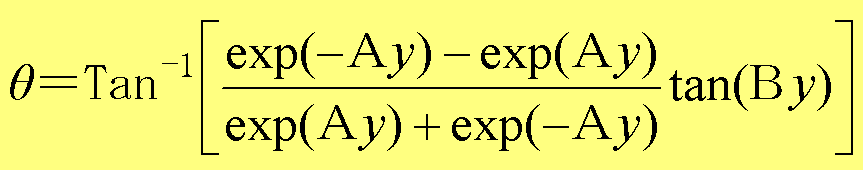 (1.51)
(1.51)
 (1.52)
(1.52)
であり、
S=(y2+b2)/2σy+θ(y) +(xに依存する項) (1.53)
となる。さて、(1.53)をyで偏微分すればy方向の運動量(m=1なので、速度と同じ)が求まるが、その前に(1.52)の絶対値(複素共役との積)を求めてみる。これは、粒子の確率分布に比例するはずである。
(Ψ1+Ψ2)(Ψ1+Ψ2)*=g(x)g(x)*exp{-2(y2+b2)(Δy)2/σy}{exp(2Ay)+exp(-2Ay)+2cos(2By)} (1.54)
ここから、yに依存する部分だけを取り出せば
P(y,t)∝exp{-2(y2+b2)(Δy)2/σy}{exp(2Ay)+exp(-2Ay)+2cos(2By)} (1.55)
となる。なお、ここで「=」ではなく「∝」となっているのは、波動関数を規格化していないためである。このP(y)を時間毎にプロットすると、図1.5.2のようになる。
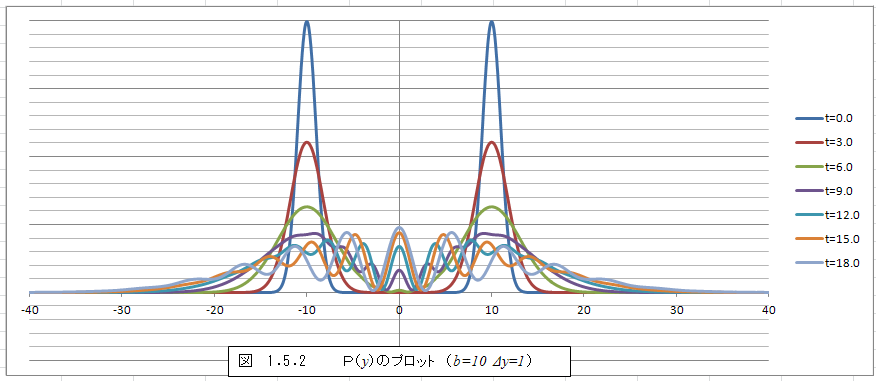
最初は、b=10及びb=-10の周りに集中しているが、時間が経つにつれて分布が広がって行き、干渉を起こす様子がわかる。なお、図1.52はyを0.1ずつの間隔で-50.0~50.0までとり、P(y)をプロットしたものの一部であるが、時間t毎に規格化定数が異なるためy=-50.0からy=50.0までの式(1.55)右辺の総和を求め(これは近似的に積分範囲-50.0~50.0で∫P(y)dyを計算することにあたる)、その総和で除算した上でプロットしている。図1.52からわかるように、全ての時間においてyの絶対値が40となる辺りでP(y)がほとんど0になることから、規格化は概ね正確である。従って、図1.52はtが異なっていても確率分布として比較することができる。
さて、図1.5.2でt=0.0の曲線についてy=10.0近辺のみをプロットすると、図1.5.3のようになる。
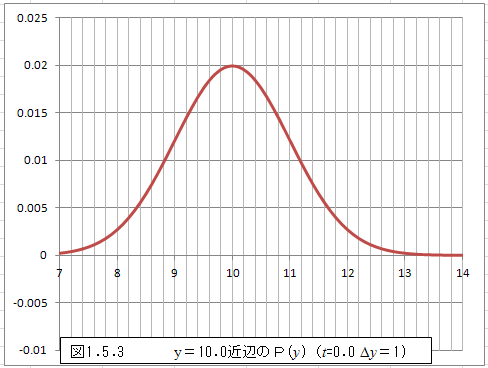
図1.5.3によると概ねΔy=1の4倍~6倍程度の範囲(原点に近い領域でy=7.0~8.0)で確率分布が小さくなることがわかる。これは、シミュレーションをする際にスリットの幅をΔyに対してどの程度に設定すべきかということに関係する。これによると、Δyに対して4倍~6倍程度に設定するのが妥当であることがわかる。
さて、いよいよ式(1.53)をyで偏微分し、y方向の運動量(=y方向の速度:m=1)を求めると、
py=∂S/∂y=(∂/∂y){(y2+b2)/2σy+θ(y) +(xに依存する項)}=y/σy+∂θ(y)/∂y
となる。そして、式(1.51)より、非常に煩雑な∂θ(y)/∂y計算を行うと、
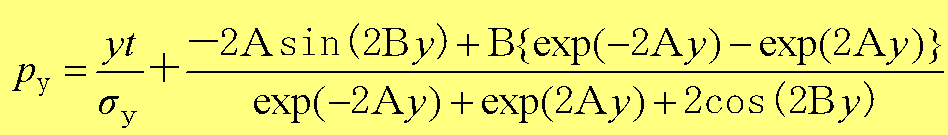 (1.56)
(1.56)
σy=4((Δy)4+t2/4) A=2b(Δy)2/σy B=bt/σy
となる。
続いて、x方向であるが、式(1.47)のg(x)に相当する部分は、前節の式(1.29)と同じである。x方向とy方向を独立するものとして波動関数を設定しているため、当然の結果である。従って、x方向の軌跡は解析的に求めることが可能であり、前節の式(1.37)より、
x=x1/2(Δx)2・(t2+4(Δx)4)1/2+kxt (1.57)
となる。なお、x1がt=0における粒子のx座標となる。
1.5.2 シミュレーションの実行
式(1.56)と式(1.57)を用いれば、2重スリットのシミュレーションが可能になる。x方向は、解析に解が判っているので特に近似計算をする必要はない。式(1.56)については、次のようにして粒子軌道を計算する。
①t=0におけるyの初期値y0を設定する。
②式(1.56)のpyはm=1としていることから、これは時間と位置により与えらえる速度と見なすことができるため、
ある時間tiにyiにある粒子の速度をv(ti,yi)と表し、時間の刻みをΔtとすれば、
yi+1=v(ti,yi)Δt+
yi
により、y0から順次任意の時刻における粒子の位置が求まる。
あまり、精密な近似ではないが、これにより粒子のy方向の位置をシミュレートする。
なお、初期値の設定はΔy=1とし、y軸の正座標側をy=bの周りにb-a/2≦y0≦b+a/2、y軸の負座標側をy=-bの周りに-b-a/2≦y0≦-b+a/2として与えることとし、aがスリットの幅に相当する。図1.53の後で説明したように、aはΔy=1の4倍~6倍程度の大きさとする。また、kx=0.4とする。
続いて、x方向の運動については、式(1.57)でx1=0としてまずはシミュレーションを行う。理由は、このように扱うと粒子の軌跡が判り易くなることと、『THE UNDIVIDED UNIVERSE』の中で紹介されているものと同様の軌跡が得られるためである。なお、後ほどx1の値を0以外とした場合の軌跡についても、実際にシミュレートし結果を示す。
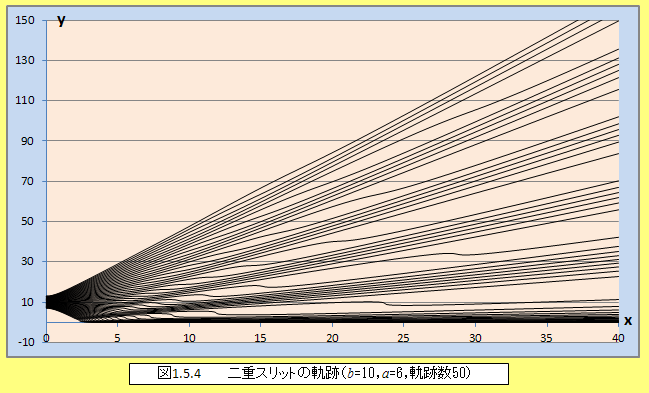
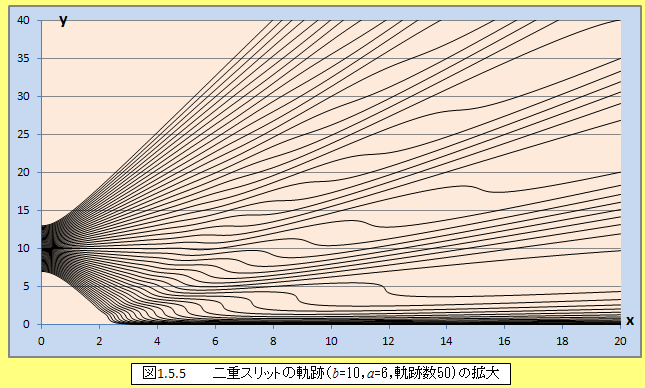
まず、図1.5.4は、スリットの幅(a)=6.00,スリットの間隔(2b)=20.00,時間の刻みΔt=0.002とし、粒子の軌跡50本をt=0~100までプロットしたものである。初期値となる粒子の位置は、y0=7.00~13.00の範囲で等間隔に設定した。軌跡の片側だけをプロットしたものであるが、粒子が干渉のような粗密性のある軌道を辿ることがわかる。続いて、図1.5.5は図1.5.4を拡大したものである。粒子がどのような運動をし、干渉像を形成するかがわかるであろう。
なお、図1.5.6と図1.5.7は、図1.5.4と図1.5.5の軌跡の両方を表したものである。当然のことながら、yが正の領域と負の領域が対称になっていることがわかる。
図1.54~図1.57のどの図も、初期値(y0)が異なる軌道が多数描かれているのであり、決して流体のようなものではない。粒子の実在を仮定するボーム力学では、スリットを通った1つの粒子が、このような軌道の1つを辿る運動をする。従って、どちらかのスリットを粒子が通ったとすることができ、さらに粒子がどちらかのスリットを通ることと干渉像が生じることの間に矛盾が生じない。ただし、初期値を確定することができないため、どの軌道を実際に粒子が辿るのかは予測することはできない。
粒子の実在を肯定し、粒子の不可分性を保ち、干渉像が表れることが説明できるという意味で、二重スリットの問題に対して「ドブロイ=ボーム解釈」は直観的な理解が得やすい。


1.5.3 二重スリットの量子ポテンシャル
シミュレーションの方法が確立されたのだから、様々な条件を設定して結果を示したいところであるが、それは次節に先送りすることとし、二重スリットの量子ポテンシャルを求め本節の締めくくりとする。そのためには、式(1.52)を式(1.1) Ψ(r,t)=Rexp(iS) に当てはめてRを求め、それを式(1.6)Q =-(1/2m)(∇2R /R) に代入し計算しなければならない。なお、x方向に関係する部分は前節のガウス波束と同じあるため求めない。
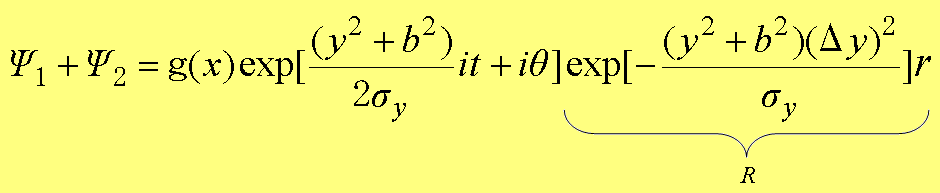
r={exp(2Ay)+exp(-2Ay)+2cos(2By)}1/2
上記は、式(1.52)を再掲載し、Rに該当する部分を示したものである。これを、式(1.6)Q =-(1/2m)(∇2R /R)に代入し直接計算するのは、非常に複雑であるため、形式的にRを
R=exp{-y2(Δy)2/σy}(f(y))1/2 (f(y)≧0) (1.58)
とおき計算することとする。
まず、
∂R/∂y={-2y(Δy)2/σy+1/2f・∂f/∂y}R
∂2R/∂y2={-2(Δy)2/σy-1/2f2・(∂f/∂y)2+1/2f・∂2f/∂y2}R+{-2y(Δy)2/σy+1/2f・∂f/∂y}∂R/∂y
={-2(Δy)2/σy-1/2f2・(∂f/∂y)2+1/2f・∂2f/∂y2}R+{-2y(Δy)2/σy+1/2f・∂f/∂y}2R
∴(∂2R/∂y2)/R=-2(Δy)2/σy-1/2f2・(∂f/∂y)2+1/2f・∂2f/∂y2+{-2y(Δy)2/σy+1/2f・∂f/∂y}2
=-2(Δy)2/σy-1/4f2・(∂f/∂y)2+1/2f・∂2f/∂y2+4y2(Δy)4/σy2-2y(Δy)2/f・∂f/∂y
=-2(Δy)2/σy-1/4・{(∂f/∂y)/f}2+1/2・(∂2f/∂y2)/f+4y2(Δy)4/σy2-2y(Δy)2(∂f/∂y)/f
となる。よって、式(1.6)Q =-(1/2m)(∇2R /R)より、m=1の場合に量子ポテンシャルは、
Q =(Δy)2/σy+1/8・{(∂f/∂y)/f}2- 1/4・(∂2f/∂y2)/f-
2y2(Δy)4/σy2+y(Δy)2(∂f/∂y)/f
f=exp(2Ay)+exp(-2Ay)+2cos(2By)
∂f/∂y=2A{exp(2Ay)-exp(-2Ay)}- 4Bsin(2By)
∂2f/∂y2=4A2{exp(2Ay)+exp(-2Ay)}- 8B2cos(2By)
σy=4((Δy)4+t2/4) A=2b(Δy)2/σy B=bt/σy (1.59)
となる。
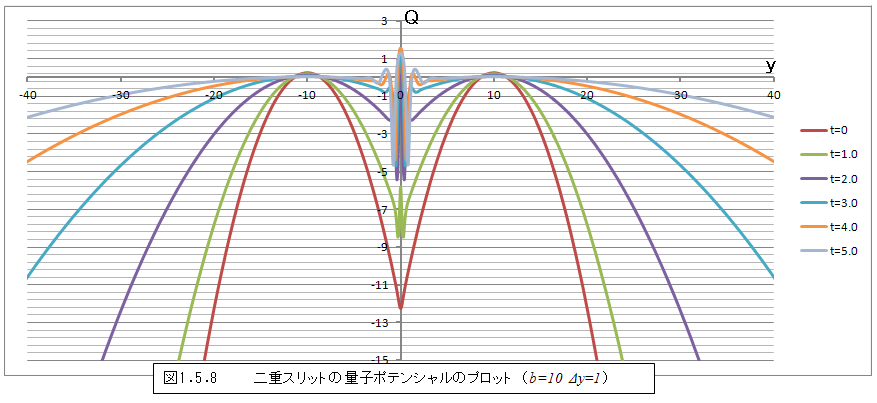
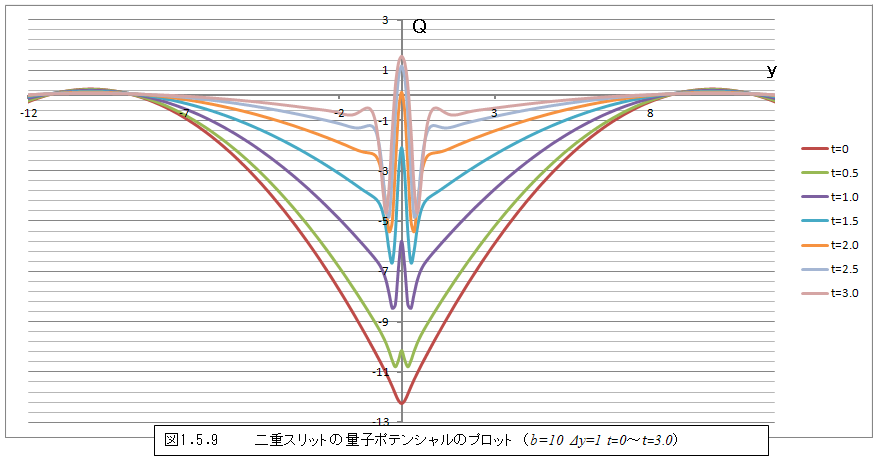
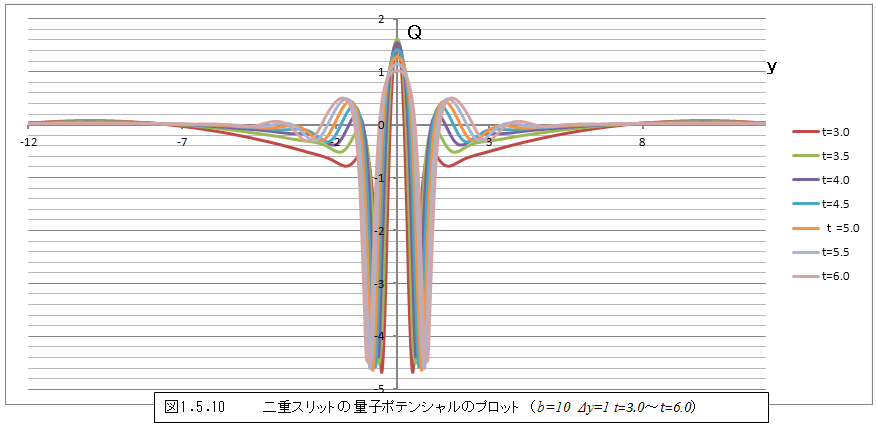
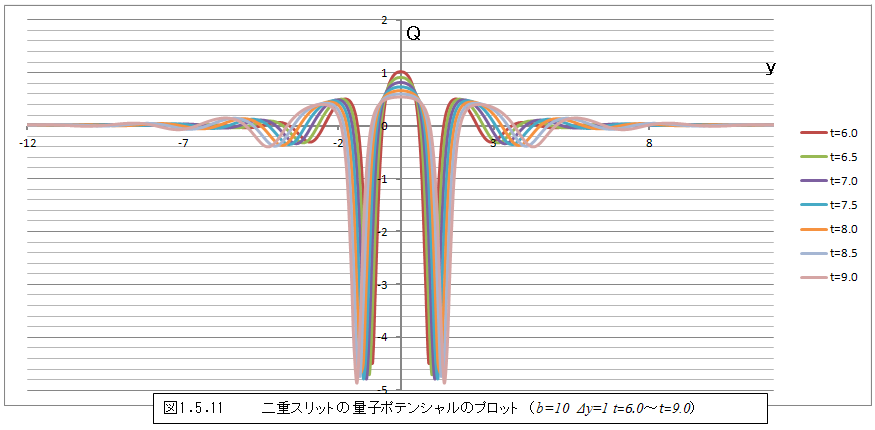
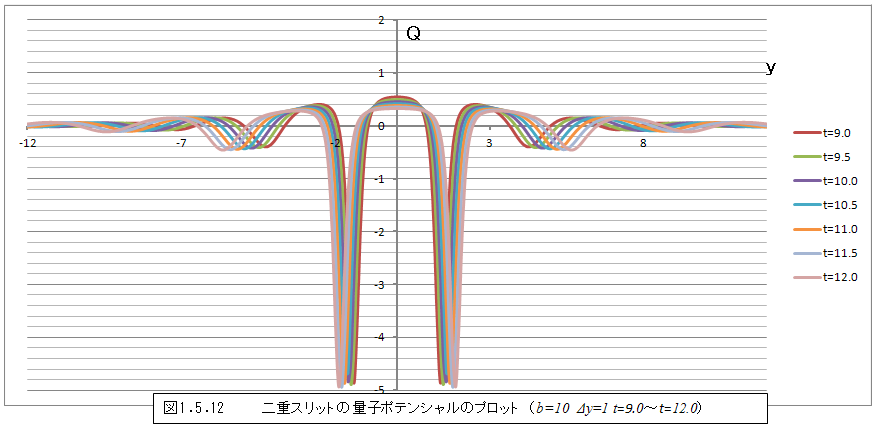
さて、こうして得られた量子ポテンシャルを時間毎にグラフに表してみると、図1.5.8のようになる。t=0では単純な形であるが時間が経つにつれて、y=0の周囲から徐々に複雑な形状に変化していることがわかる。変化の様子をもう少し詳細に見るために、時間の間隔を小さくし、y=0の周囲のみをグラフにすると図1.5.9~図1.5.12のような変化になる。
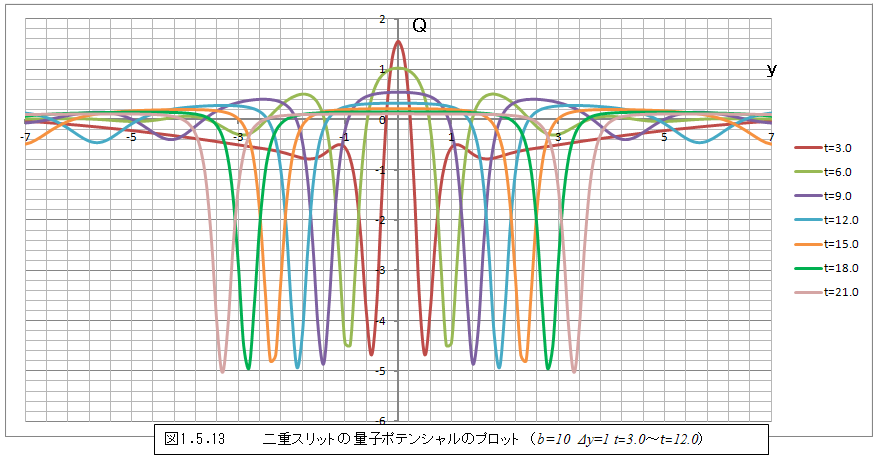
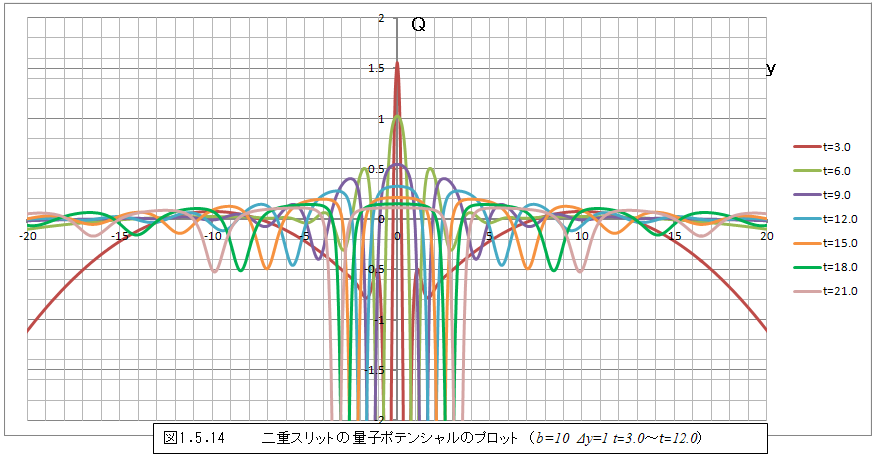
t=3.0以降では変化が小さくなるため、図1.5.10~図1.5.12では変化がわかりにくい。そこで、時間の間隔を大きくしグラフにすると、図1.5.13・図1.5.14のようになる。
簡単に言って、t=0にy=0で発生した量子ポテンシャルの複雑な変化が全体に伝わっていく過程と、前節のように徐々に量子ポテンシャルが0に近づいていく過程が重ね合わさったような変化であることがわかる。なお、図1.5.13の極小部の変化から、概ね前者の変化が伝わる速さは光速の40%程度であることがわかる。(原子単位系では、速さ1が光速になる)
次節では、様々条件で行ったシミュレーションの結果を示すこととする。
アマチュアリズムの量子力学